Identify linear equations
Key Notes:
A function whose graph is a straight line is a linear function.
The graph of a nonlinear function is not a straight line.
Learn with an example
The graph shows a function. Is the function linear or nonlinear?
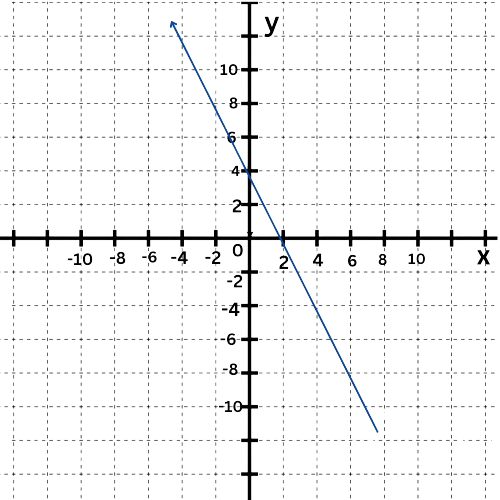
- Linear
- Non-linear
To determine whether the function is linear or nonlinear, see whether the graph is a straight line.
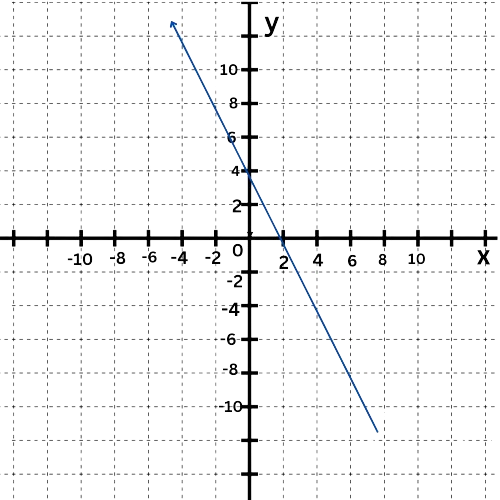
The graph is a straight line.
So, the function is linear.
The graph shows a function. Is the function linear or nonlinear?
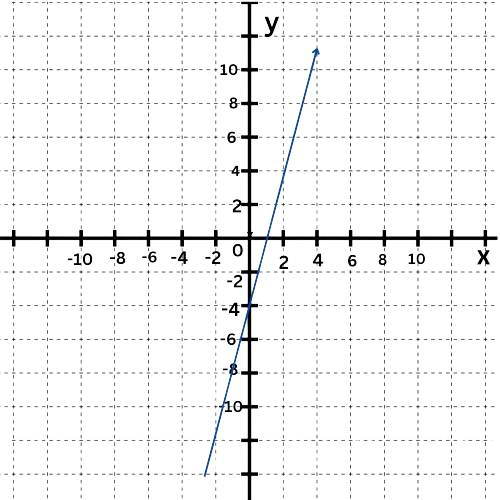
- Linear
- Non-linear
To determine whether the function is linear or nonlinear, see whether the graph is a straight line.
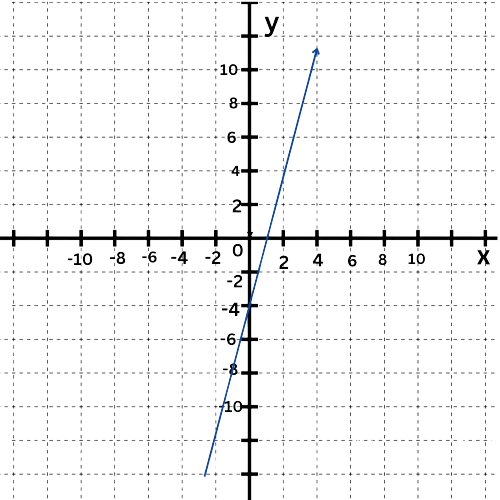
The graph is a straight line.
So, the function is linear.
Let’s Practice!
