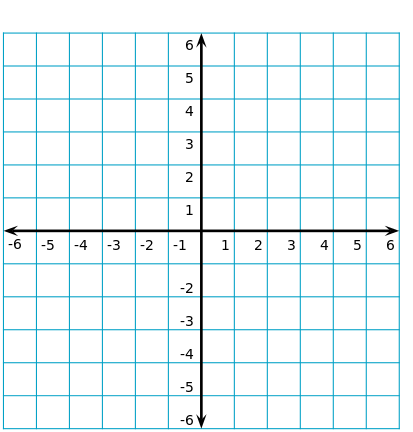
Quadrants and axes
Key Notes :
1. Introduction to the Coordinate Plane
- Coordinate Plane: A two-dimensional plane formed by the intersection of two perpendicular number lines called the x-axis (horizontal) and y-axis (vertical).
- Axes:
- X-Axis: The horizontal axis.
- Y-Axis: The vertical axis.
- Origin: The point of intersection of the x-axis and y-axis, denoted as (0, 0).
2. Understanding Coordinates
- Ordered Pairs: Coordinates are written as ordered pairs (x, y), where ‘x’ is the position on the x-axis and ‘y’ is the position on the y-axis.
- Example: (3, 4) means moving 3 units along the x-axis and 4 units up the y-axis.
3. The Four Quadrants
The coordinate plane is divided into four quadrants:
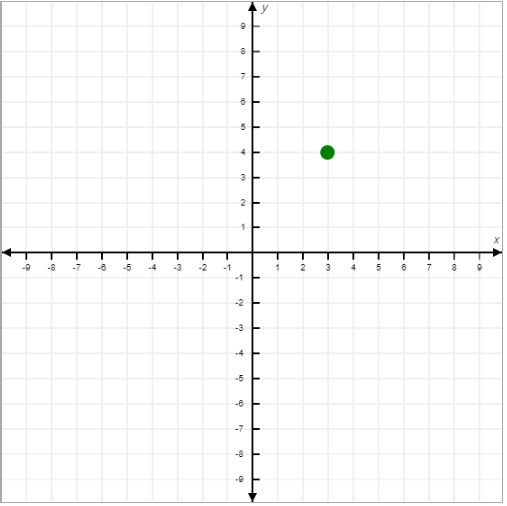
- First Quadrant:
- Location: Top-right section.
- Sign of Coordinates: Both x and y are positive (x > 0, y > 0).
- Example: (2, 5).
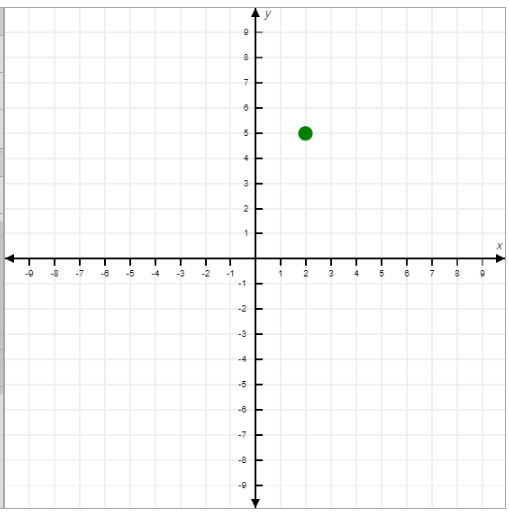
- Second Quadrant:
- Location: Top-left section.
- Sign of Coordinates: x is negative, y is positive (x < 0, y > 0).
- Example: (-3, 4).
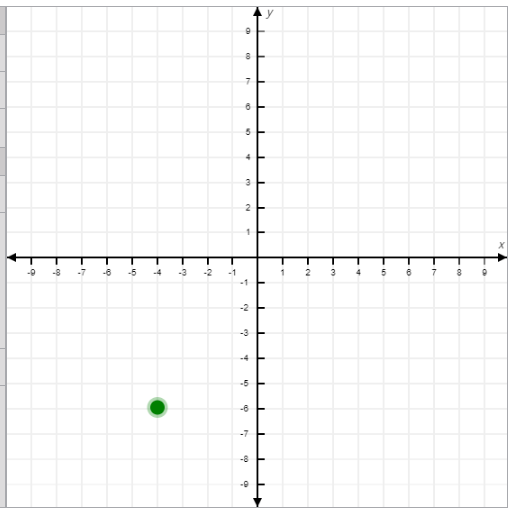
- Third Quadrant:
- Location: Bottom-left section.
- Sign of Coordinates: Both x and y are negative (x < 0, y < 0).
- Example: (-4, -6).
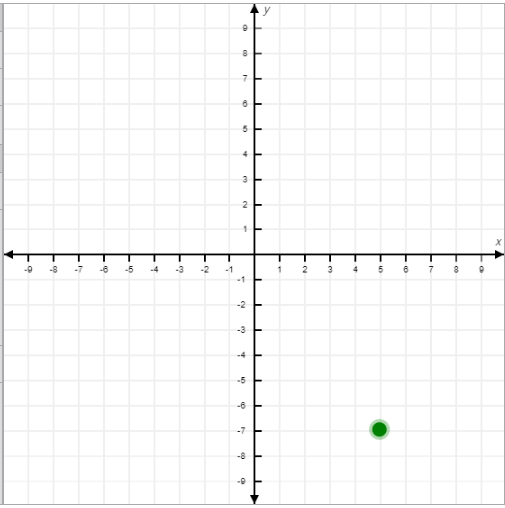
- Fourth Quadrant:
- Location: Bottom-right section.
- Sign of Coordinates: x is positive, y is negative (x > 0, y < 0).
- Example: (5, -7).
4. Axes and Points on Axes
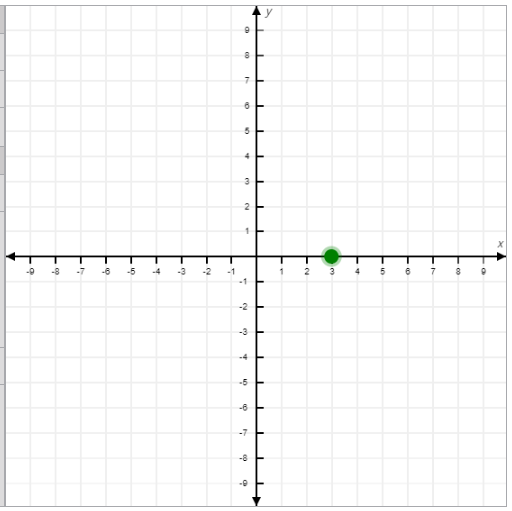
- Points on the X-Axis:
- Have coordinates of the form (x, 0), meaning they lie directly on the x-axis.
- Example: (3, 0) lies 3 units to the right of the origin.
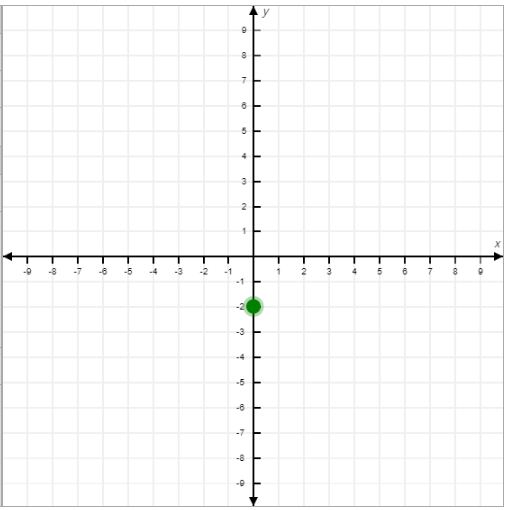
- Points on the Y-Axis:
- Have coordinates of the form (0, y), meaning they lie directly on the y-axis.
- Example: (0, -2) lies 2 units below the origin.
5. Plotting Points
- Steps to Plot a Point:
- Start at the origin (0, 0).
- Move horizontally along the x-axis according to the x-coordinate.
- Move vertically along the y-axis according to the y-coordinate.
- Mark the point where these positions intersect.
6. Examples
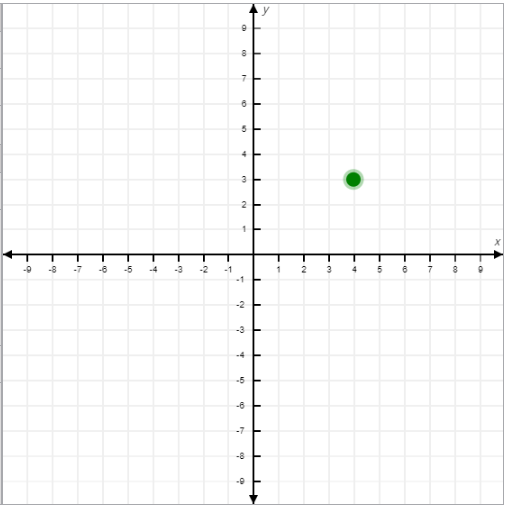
- Example 1: Plot the point (4, 3).
- Move 4 units right along the x-axis and 3 units up along the y-axis.
- The point lies in the first quadrant.
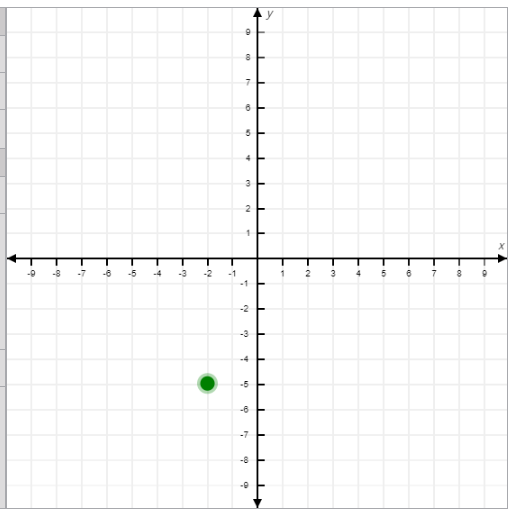
- Example 2: Plot the point (-2, -5).
- Move 2 units left along the x-axis and 5 units down along the y-axis.
- The point lies in the third quadrant.
7. Significance of Quadrants
- Symmetry: Understanding the quadrants helps in identifying the symmetry of points with respect to the axes and origin.
- Graphing Functions: Quadrants are used to graph linear and non-linear functions, understanding the behavior of the graph in different quadrants.
- Real-Life Applications: Used in mapping, physics (vector representation), economics (demand and supply analysis), and many other fields.
8. Common Mistakes to Avoid
- Confusing Signs: Misinterpreting the signs of the coordinates can place points in the wrong quadrant.
- Origin Misplacement: Failing to start plotting from the origin can lead to incorrect positioning of points.
- Axes Mix-Up: Confusing the x and y coordinates can lead to incorrect graphing.
Learn with an example
Which point is in Quadrant IV?
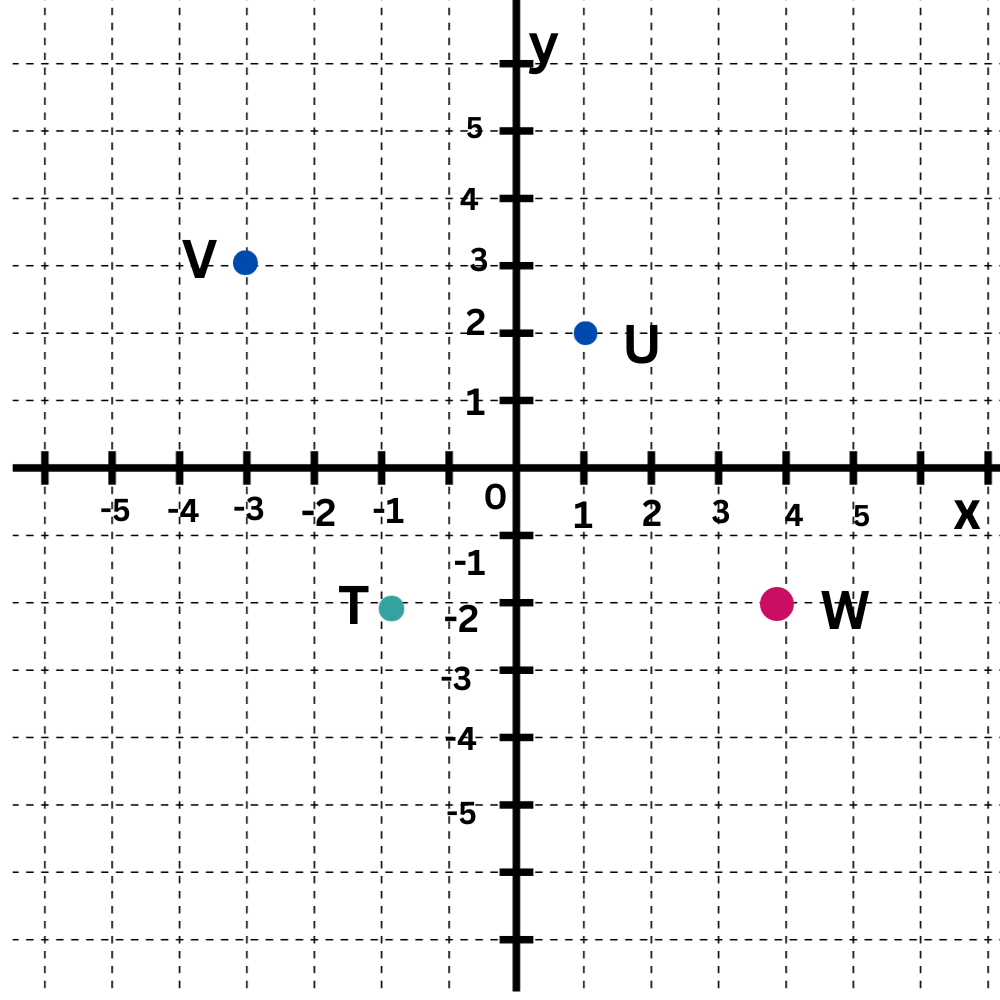
Quadrant IV is the bottom right quadrant.
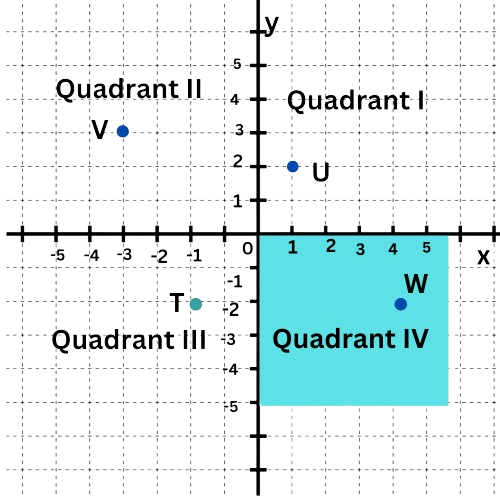
Which point is in Quadrant IV?
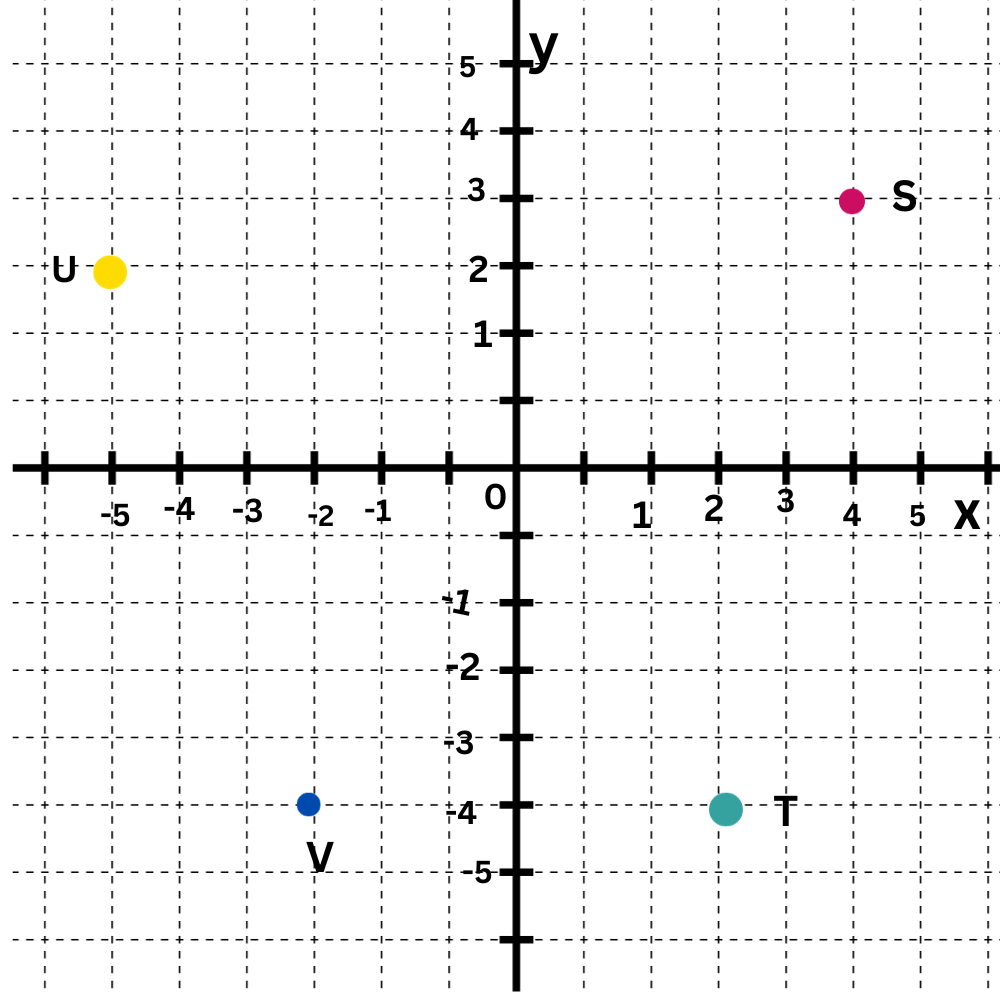
- S
- T
- U
- V
Quadrant IV is the bottom right quadrant.
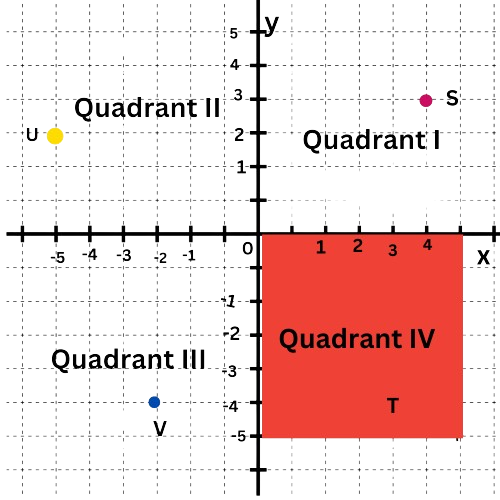
The point T is in Quadrant IV.
Let’s practice!

