Write and solve equations that represent diagrams

key points :

Understanding the Diagram:

  • Read the diagram carefully.
  • Identify variables (unknowns) represented by symbols (like x, y).
  • Look for shapes, lines, or symbols that represent operations (e.g., addition, subtraction).

Translate Visual Information into an Equation:

  • Use the relationships shown in the diagram to form an equation.Convert visual cues (like boxes or arrows) into mathematical operations.Assign a variable to the unknown value.
Example: If a box shows “x + 3 = 7”, write it directly as an equation.

Write the Equation:

Use appropriate mathematical symbols (+, −, ×, ÷).

Write one equation per relationship shown.

Ensure both sides of the equation are balanced.

Solve the Equation:

  • Use inverse operations (add ↔ subtract, multiply ↔ divide) to isolate the variable.Solve step by step and check your work.
Example:
x + 3 = 7
Subtract 3 on both sides: x = 4

Label the Answer:

Include units if mentioned in the diagram (e.g., cm, kg, dollars).

Interpret your solution in the context of the problem.

✏️ Tips for Solving Diagram-Based Equations:

  • Look for patterns or repeated steps.
  • Break complex diagrams into smaller parts.
  • Draw your own version if the diagram is confusing.
  • Use substitution if there’s more than one variable.

🧠 Example Problem:

A diagram shows:
A box labeled “x”, followed by an arrow and the instruction “Add 5”, then another arrow to a box labeled “Result: 12”.

👉 Equation:
x+5=12

👉 Solution:
x=12−5=7

Learn with an example

Write an equation that says that the length of the green line is equal to the length of the black line. Combine like terms.

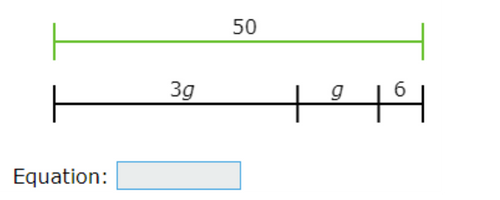
We want to replace both sides of the equation below with numbers and variable expressions:

length of green line=length of black line

The length of the green line is 50.

The black line is the sum of its segments, so:

length of black line=3g+g+6

=4g+6

Putting these together gives:

50=4g+6

Write an equation that says that the length of the green line is equal to the length of the black line. Combine like terms.

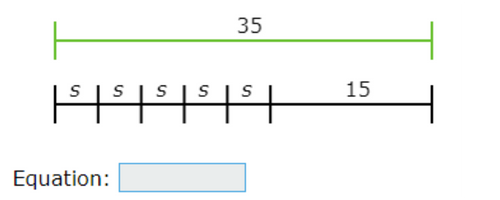
We want to replace both sides of the equation below with numbers and variable expressions:

length of green line=length of black line

The length of the green line is 35.

The black line is the sum of its segments, so:

length of black line=s + s + s + s + s + 15

=5s+15

Putting these together gives:

35=5s+15

Write an equation that says that the length of the green line is equal to the length of the black line. Combine like terms.

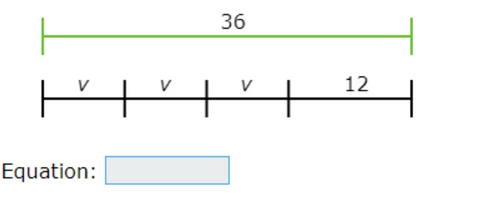
We want to replace both sides of the equation below with numbers and variable expressions:

length of green line=length of black line

The length of the green line is 36.

The black line is the sum of its segments, so:

length of black line = v + v + v + 12

= 3v + 12

Putting these together gives:

36 = v + 12

let’s practice!