Model and solve equations using algebra tiles
key notes :
What Are Algebra Tiles?
Algebra tiles are manipulatives used to visually represent algebraic expressions and equations.
Types of tiles:
- Unit tile (small square) = 1
- x-tile (rectangle) = x
- x²-tile (large square) = x²
- Negative tiles are usually red or a different color.
Purpose of Using Algebra Tiles
- Helps students visualize and understand abstract algebraic concepts.
- Makes it easier to model equations, simplify expressions, and solve equations step by step.
Modeling Expressions
- Represent algebraic expressions like x + 3, 2x – 1, using a combination of positive and negative tiles.
- Positive x → green rectangle, Negative x → red rectangle.
- Positive 1 → green square, Negative 1 → red square.
Setting Up the Equation
- Use a mat or draw a balance scale to model both sides of an equation (e.g., x + 3 = 2x – 1).
- Place corresponding tiles on each side of the equal sign to represent each expression.
Solving the Equation
- Step 1: Use zero pairs to eliminate tiles on both sides (e.g., +x and -x cancel each other).
- Step 2: Isolate the variable tile on one side of the equation.
- Step 3: Balance the equation by adding/removing tiles equally on both sides.
- Step 4: Count the number of unit tiles to find the value of x.
Zero Pairs
- A positive tile and a negative tile together form a zero pair (e.g., +1 and -1 = 0).
- Used to eliminate tiles and keep the equation balanced.
Check Your Solution
- After finding the value of x, substitute it back into the original equation to verify.
Advantages for Students
- Builds conceptual understanding before abstract methods.
- Enhances problem-solving and logical reasoning skills.
✏️ Example:
Solve x + 2 = 3 using algebra tiles:
- Left side: 1 x-tile + 2 unit tiles.
- Right side: 3 unit tiles.
- Remove 2 unit tiles from both sides.
- Left: 1 x-tile, Right: 1 unit tile → So, x = 1.
Learn with an example
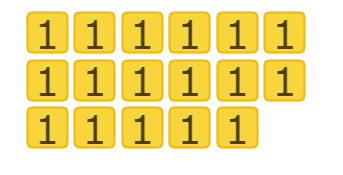
Which equation does this set of algebra tiles represent?
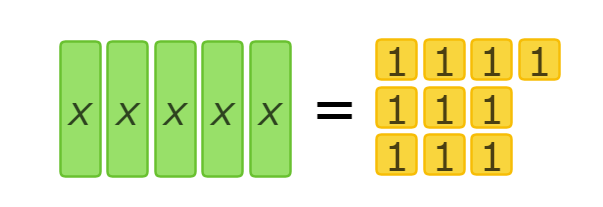
- 8x = 8
- 7x = 7
- 2x = 10
- 5x = 10
Look at the tiles on the left side of the set.
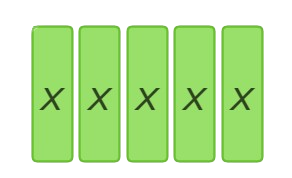
The left side has 5 (x) tiles. So, the left side of the equation should be 5x.
Now look at the tiles on the right side of the set.
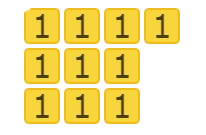
The right side has 10 (1) tiles. So, the right side of the equation should be 10.
This set of algebra tiles represents the equation 5x=10.
Which equation does this set of algebra tiles represent?
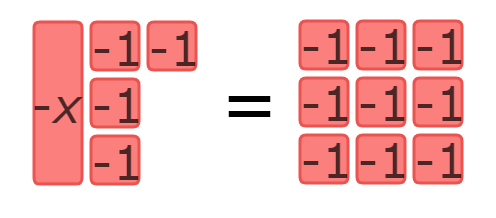
- – X – 4 = 8
- – X – 4 = -9
- – X – 4 = 4
- – X – 4 = 17
Look at the tiles on the left side of the set.
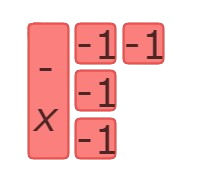
The left side has 1(-x ) tile and 4 (-1) tiles. So, the left side of the equation should be –x–4.
Now look at the tiles on the right side of the set.
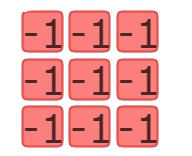
The right side has 9(-1) tiles. So, the right side of the equation should be–9.
This set of algebra tiles represents the equation –x–4=–9.
Which equation does this set of algebra tiles represent?
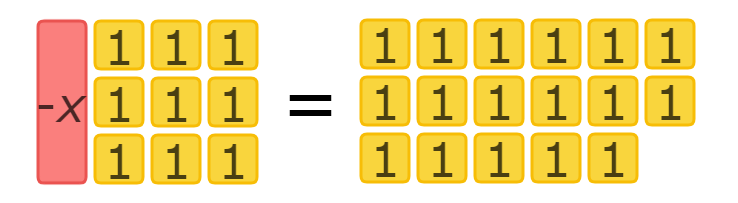
- – X – 4 = 17
- – X – 7 = 17
- – X + 9 = 17
- – X – 5 = 17
Look at the tiles on the left side of the set.
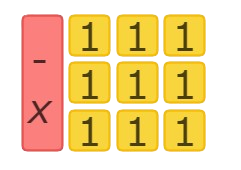
The left side has 1 (-X) tile and 9 (1) tiles. So, the left side of the equation should be – X+9.
Now look at the tiles on the right side of the set.
The right side has 17(1) tiles. So, the right side of the equation should be 17.
This set of algebra tiles represents the equation – X + 9 = 17.
Let`s practice!

