Construct the midpoint or perpendicular bisector of a segment

Key Notes :

https://i.ytimg.com/vi/IQ35R6CWqd8/maxresdefault.jpg?utm_source=chatgpt.com
https://i.ytimg.com/vi/jDswTWpBmWI/sddefault.jpg?utm_source=chatgpt.com

🔹 Basic Terms to Know

  • Line segment: A part of a line with two endpoints.
  • Midpoint: The point that divides a line segment into two equal parts.
  • Perpendicular bisector: A line that
    ✔ cuts a segment into two equal parts
    ✔ meets the segment at 90° (right angle).

🔹 Construction Tools

  • Compass
  • Ruler (straightedge)
    ❌ Do not measure lengths with the ruler.

✏️ Construction of the Midpoint of a Line Segment

Let the line segment be AB.

  1. Place the compass at A and draw arcs above and below the segment.
  2. Without changing the compass width, place it at B and draw arcs cutting the previous arcs.
  3. Join the two intersection points of the arcs.
  4. The line drawn cuts AB at point M.
  5. M is the midpoint of segment AB.

👉 This line is also the perpendicular bisector.

✏️ Construction of the Perpendicular Bisector

For the same segment AB:

  1. With A as centre, draw arcs on both sides of the segment.
  2. With B as centre and the same radius, draw arcs intersecting the first pair.
  3. Join the intersection points.
  4. The line obtained:
    • is perpendicular to AB
    • bisects AB into two equal parts.

🔹 Important Properties

  • The perpendicular bisector always passes through the midpoint.
  • Any point on the perpendicular bisector is equidistant from A and B.
  • Construction is accurate and better than measurement.

🧠 Exam Tips

  • Always show construction arcs clearly.
  • Label points neatly (A, B, M).
  • Mention steps in logical order.
  • Do not erase construction lines unless instructed.

Learn with an example

Mark the midpoint of AB ?

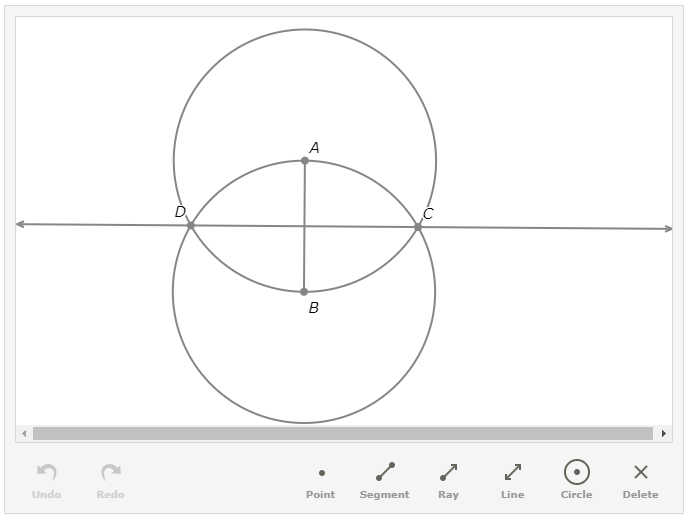
Part of the construction was done for you. Here are the steps to create this part of the construction.

Start with the objects in the diagram below.

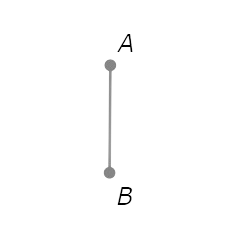
  • Draw a circle with radius AB centred at A.
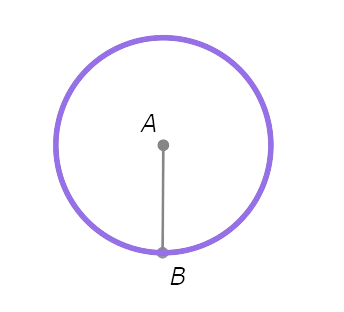
  • Draw a circle with radius AB centred at B.
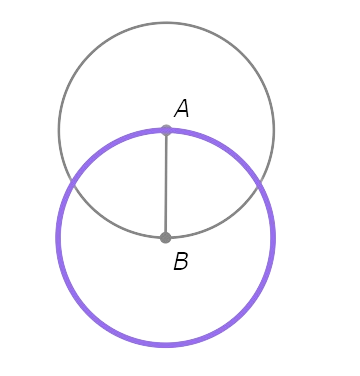
  • Mark the points where ⨀A and ⨀B intersect. Call them C and D.

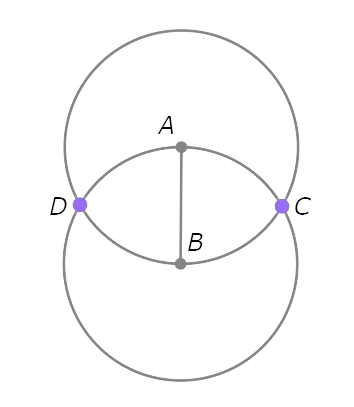
Since B and C are both on ⨀A, AB=AC. Since A and C are both on ⨀B, AB=BC. So, AB=AC=BC.

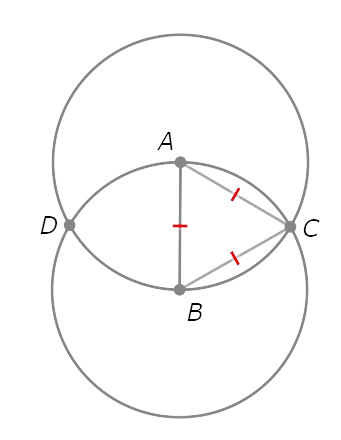
Similarly, AB=AD=BD.

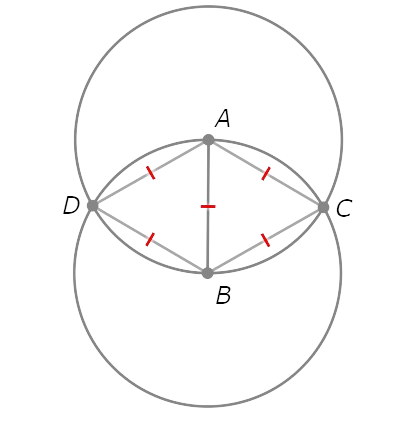
So, C and D are equidistant from A and B.

  • Draw the line through C and D.

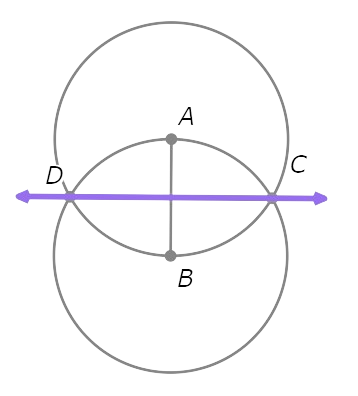
Recall that the set of points equidistant from A and B form the perpendicular bisector of AB. Since C and D are equidistant from A and B, they lie on the perpendicular bisector. So , CD is the perpendicular bisector of AB.

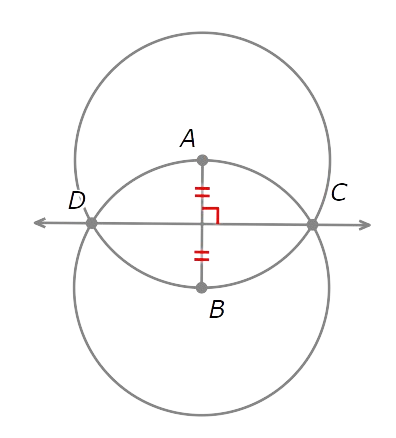
Complete the construction.

To complete the construction of the midpoint o f AB , carry out the following step:

  • Mark the point where CD and AB intersect. Call it E.

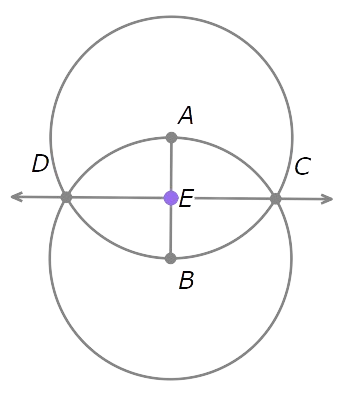
Since CD is the perpendicular bisector of AB, the intersection E is the midpoint of AB.

Mark the midpoint of AB?

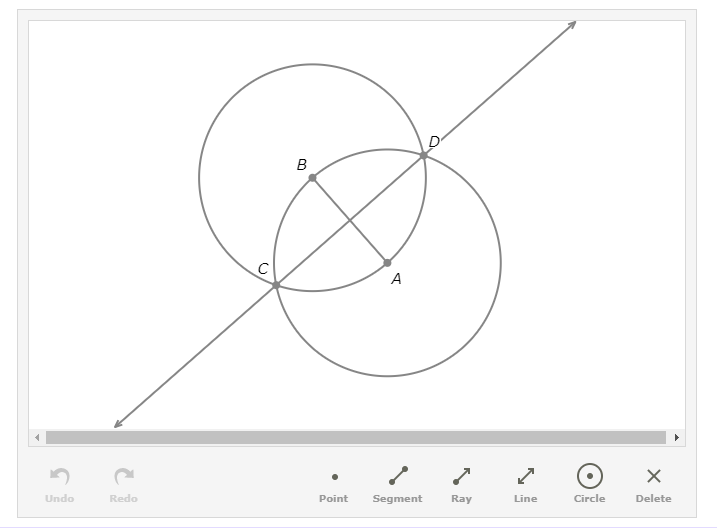
Part of the construction was done for you. Here are the steps to create this part of the construction.

Start with the objects in the diagram below.

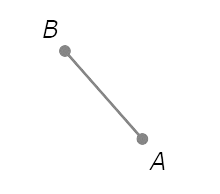
  • Draw a circle with radius AB centred at A.
  • Draw a circle with radius AB centred at B.
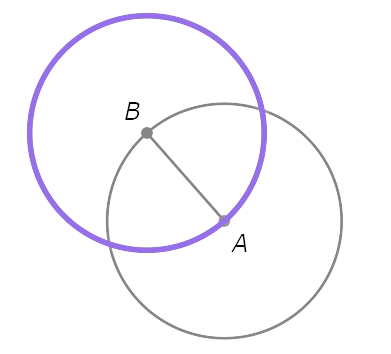
  • Mark the points where ⨀A and ⨀B intersect. Call them C and D.

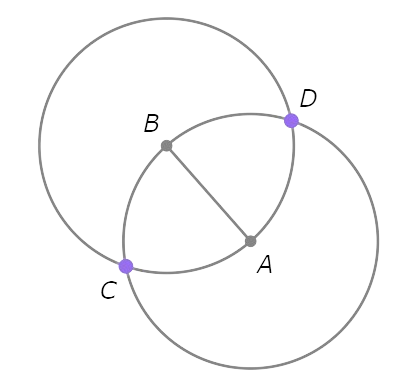
Since B and C are both on ⨀A, AB=AC. Since A and C are both on ⨀B, AB=BC. So, AB=AC=BC.

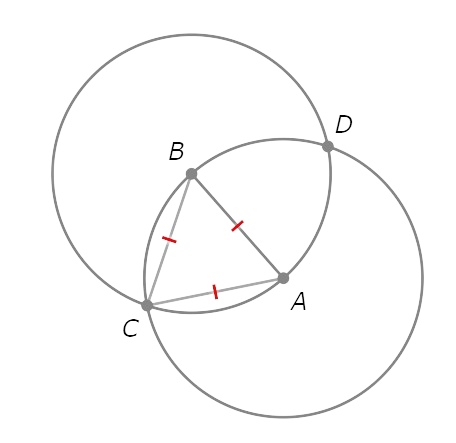
Similarly, AB=AD=BD.

So, C and D are equidistant from A and B.

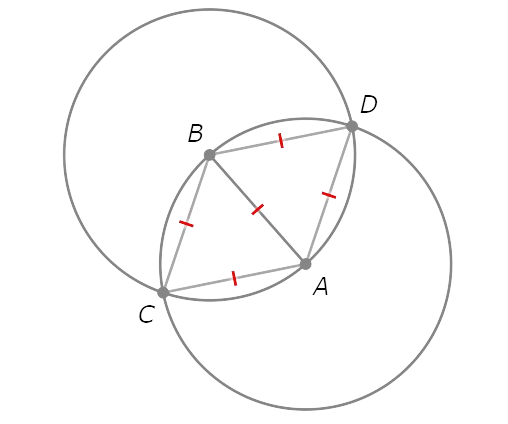
  • Draw the line through C and D.

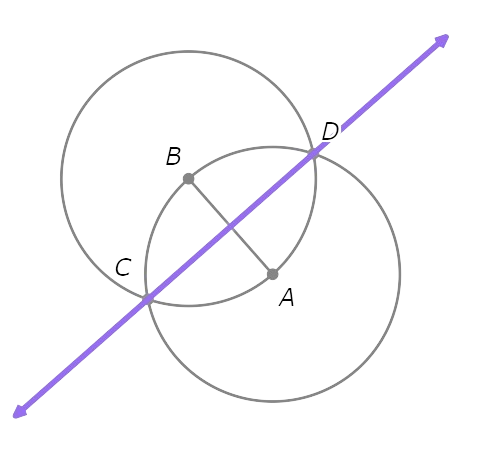
Recall that the set of points equidistant from A and B form the perpendicular bisector of AB . Since C and D are equidistant from A and B, they lie on the perpendicular bisector. So , CD is the perpendicular bisector of AB.

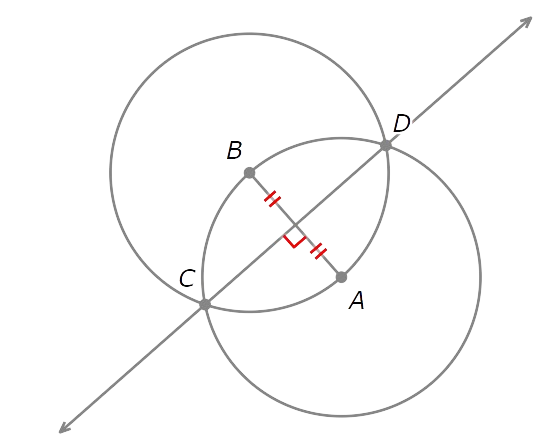
Complete the construction.

To complete the construction of the midpoint of AB , carry out the following step:

  • Mark the point where CD and AB intersect. Call it E.

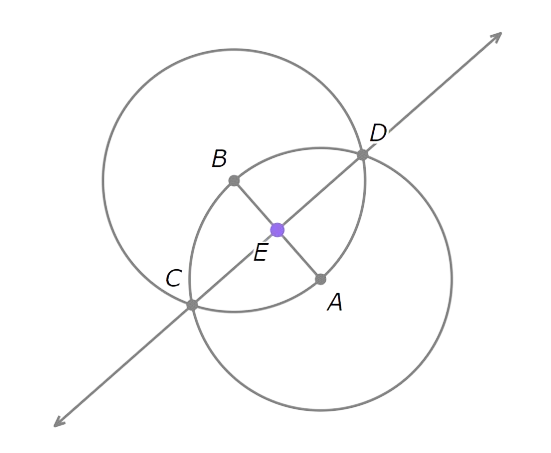
Since CD is the perpendicular bisector of AB , the intersection E is the midpoint of AB.

let’s practice!