Inscribed angles

key notes :

An inscribed angle is an angle whose vertex is on a circle and whose sides are chords of the circle. The arc that lies between the two sides of an inscribed angle is called an intercepted arc.

For example, in the circle below, inscribed angle ∠Y intercepts XZ.

A circle is shown. Points X, Y, and Z all lie on the circle. Line segments XY and YZ are chords of the circle that form angle Y.

Inscribed Angle Theorem

The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of the arc it intercepts.

For example, in the circle below, m∠K= 1/2 . mLM.

Circle J is shown. Points K, L, and M all lie on the circle. Line segments KL and KM are chords of the circle that form angle K.

Another way to state the Inscribed Angle Theorem is that the measure of an inscribed angle is half the measure of the central angle that intercepts the same arc.

For example, in the circle below, m∠K= 1/2 . m∠J.

Circle J is shown. Points K, L, and M all lie on the circle. Line segments KL and KM are chords of the circle that form angle K. Radii JM and JL form central angle J.

Since every arc has the same measure as the central angle that intercepts it, the two versions of the theorem are equivalent.

Applying the Inscribed Angle Theorem

You can use the Inscribed Angle Theorem to find missing angle measures and arc measures.

Example 1

Let’s try it! Find m∠S.

A circle is shown. Points R, S, and T all lie on the circle. Line segments RS and ST are chords of the circle that form angle S. Arc RT measures 100 degrees.

Since ∠S is an inscribed angle that intercepts RT, the measure of ∠S is half the measure of RT. Write an equation and solve for m∠S.

m∠S = 1/2 . mRT Inscribed Angle Theorem

= 1/2 . 100° Plug in mRT=100°.

=50° Multiply.

So, m∠S=50°.

Example 2

Find m∠A.

Circle A is shown. Points B, C, and D all lie on the circle. Line segments BC and CD are chords of the circle that form angle C. Angle C measures 46 degrees. Radii AB and AD form central angle A.

Since ∠C is an inscribed angle that intercepts the same arc as the central angle ∠A, the measure of ∠C is half the measure of ∠A. Write an equation and solve for m∠A.

m∠C= 1/2 . m∠A Inscribed Angle Theorem

46°=1/2 . m∠A Plug in m∠C=46°.

92°=m∠A Multiply both sides by 2.

So, m∠A=92°.

Example 3

Find the value of x.

A circle is shown. Points M, N, and O all lie on the circle. Line segments MN and NO are chords of the circle that form angle N. Angle N measures 81 degrees. Arc MO measures 4x plus 2 degrees.

Since ∠N is an inscribed angle that intercepts MO, the measure of ∠N is half the measure of MO. Write an equation and solve for x.

m∠N= 1/2 mMO Inscribed Angle Theorem

81°=1/2 (4x+2)° Plug in m∠N=81° and mMO=(4x+2)°

81=1/2 . (4x+2)

81=2x+1 Apply the distributive property.

80=2x Subtract 1 from both sides.

40=x Divide both sides by 2.

So, x=40.

Example 4

Find the value of m∠X.

A circle is shown. Points W, X, Y, and Z all lie on the circle. Line segments WX and XZ are chords of the circle that form angle X. Angle X measures 2t plus 18 degrees. Line segments WY and YZ are chords of the circle that form angle Y. Angle Y measures 3t minus 7 degrees.

To find m∠X, first find the value of t. Since ∠X and ∠Y are inscribed angles that each intercept WZ, the measure of each angle is half the measure of WZ. So, ∠X and ∠Y are congruent. Write an equation and solve for t.

m∠X=m∠Y

(2t+18)°=(3t–7)° Plug in m∠X=(2t+18)° and m∠Y=(3t–7)°

2t+18=3t–7

2t+25=3t Add 7 to both sides.

25=t Subtract 2t from both sides.

Now, use the value of t to find m∠X.

m∠X=(2t+18)°

=(225+18)° Plug in t=25

=68° Simplify.

So, m∠X=68°.

Example 5

Find the value of m∠U.

A circle is shown. Points T, U, and V all lie on the circle. Line segments TU, UV, and TV are chords of the circle that form an inscribed triangle. Angle T measures 83 degrees. Arc TU measures 88 degrees.

To solve for m∠U, first find the measure of inscribed angle ∠V. Since ∠V is an inscribed angle that intercepts TU, the measure of ∠V is half the measure of TU. Write an equation and solve for m∠V.

m∠V = 1/2 mTU Inscribed Angle Theorem

= 1/2 88° Plug in mTU=88°.

=44° Multiply.

Now, find m∠U. Use the Triangle Angle-Sum Theorem, which states that the interior angles of a triangle add up to 180°.

m∠T+m∠U+m∠V=180° Triangle Angle-Sum Theorem

83°+m∠U+44°=180° Plug in m∠T=83° and m∠V=44°.

127°+m∠U=180° Add.

m∠U=53° Subtract 127° from both sides.

So, m∠U=53°.

Deriving the Inscribed Angle Theorem

To derive the Inscribed Angle Theorem, first note that there are three different ways an angle can be inscribed in a circle:

Circle O is shown. The circle has an inscribed angle. Center O lies on a side of the inscribed angle — The center of the circle lies on a side of the inscribed angle.

Circle O is shown. The circle has an inscribed angle. Center O lies inside of the inscribed angle. — The center of the circle lies inside of the inscribed angle.

Circle O is shown. The circle has an inscribed angle. Center O lies outside of the inscribed angle. — The center of the circle lies outside of the inscribed angle.

Let’s look at each case separately.

Case 1

In the circle below, show that m∠ABC= 1/2 . mAC.

Circle O is shown. Points A, B, and C all lie on the circle. Line segments AB and BC are chords of the circle that form angle B. Diameter BC passes through center O.

Start by drawing radius AO to form △ABO.

Since AO and BO are both radii of ⨀O, AO=BO. So, △ABO is isosceles and m∠ABC=m∠BAO.

By the Exterior Angle Theorem, you also know that the measures of ∠ABC and ∠BAO add up to the measure of ∠AOC. Since ∠ABC and ∠BAO have the same measure, each angle must be half of ∠AOC.

m∠ABC= 1/2 . m∠AOC

Since ∠AOC is a central angle that intercepts AC, m∠AOC=mAC. So, the measure of ∠ABC is half the measure of AC.

m∠ABC= 1/2 . mAC

Case 2

In the circle below, show that m∠ABC= 1/2 . mAC.

Circle O is shown. Points A, B, and C all lie on the circle. Line segments AB and BC are chords of the circle that form angle B. Center O lies inside of inscribed angle B.

Start by drawing a diameter with endpoint B that passes through center O. Call the other endpoint of that diameter point D.

Circle O is shown. Points A, B, C, and D all lie on the circle. Chord AB and diameter BD form angle ABD. Diameter BD and chord BC form angle DBC.

Now center O lies on a side of m∠ABD and m∠DBC. By Case 1, each of those inscribed angles measures half the measure of the arc it intercepts.

m∠ABD = 1/2 mAD

m∠DBC = 1/2 . mDC

Notice that ∠ABD and ∠DBC form ∠ABC. Similarly, AD and DC form AC. So, you can add the equations above to show that m∠ABC=1/2 mAC.

m∠ABD+m∠DBC = ( 1/2 . mAD ) + ( 1/2 . mDC )

m∠ABC = 1/2 . mAC

Case 3

In the circle below, show that m∠ABC= 1/2 mAC .

Circle O is shown. Points A, B, and C all lie on the circle. Line segments AB and BC are chords of the circle that form angle B. Center O lies outside of inscribed angle B.

Start by drawing a diameter with endpoint B that passes through center O. Call the other endpoint of that diameter point D.

Circle O is shown. Points A, B, C, and D all lie on the circle. Diameter BD and chord AB form angle DBA. Diameter BD and chord BC form angle DBC.

Now center O lies on a side of ∠DBC and ∠DBA. By Case 1, each of those inscribed angles measures half the measure of the arc it intercepts.

m∠DBC = 1/2 mDC

m∠DBA = 1/2 mDA

Notice that ∠DBA and ∠ABC form ∠DBC. Similarly, DA and AC form DC. So, you can subtract the equations above to show that m∠ABC=1/2 mAC.

m∠DBC–m∠DBA = ( 1/2 mDC ) – ( 1/2 mDA )

m∠ABC = 1/2 . mAC

You’ve derived the Inscribed Angle Theorem!

Learn with an example

What is ∠HGI?

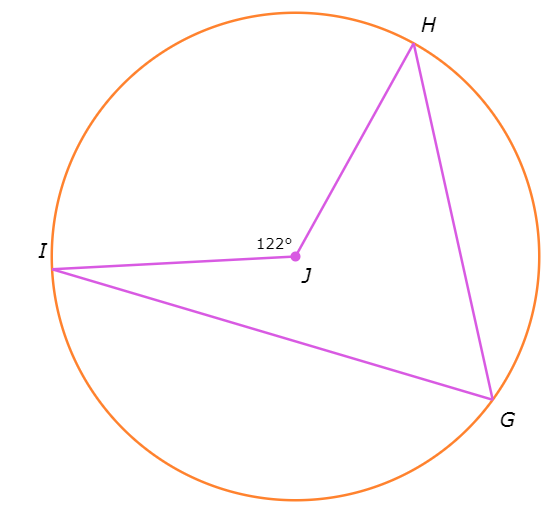
∠HGI= _____∘

Look at the diagram:

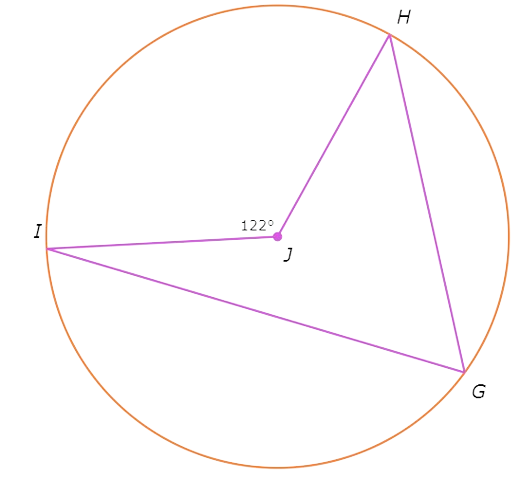
∠HGI is an inscribed angle that intercepts the same arc as the central angle ∠J, so use the Inscribed Angle Theorem.

∠HGI =1/2 . ∠j

=1/2 (122°) plug ∠J=122°

=61°

∠HGI is 61°.

What is ∠F?

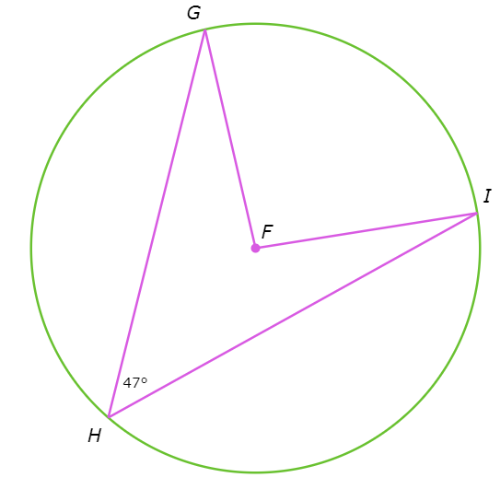
∠F= ________°

Look at the diagram:

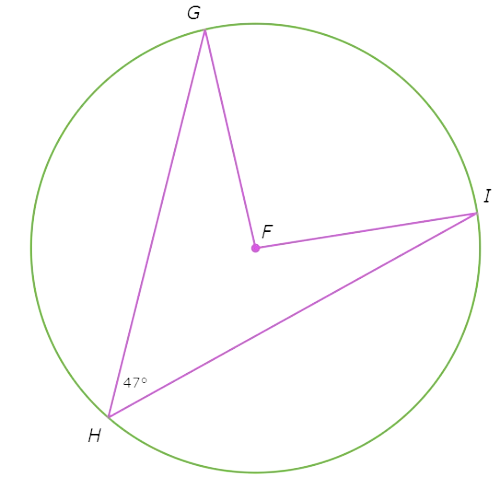
∠GHI is an inscribed angle that intercepts the same arc as the central angle ∠F, so use the Inscribed Angle Theorem.

∠F= 2 . ∠GHI Inscribed Angle Theorem

= 2 .(47°) Plug in ∠GHI=47°

= 94° Multiply

∠F is 94°.

What is ∠J?

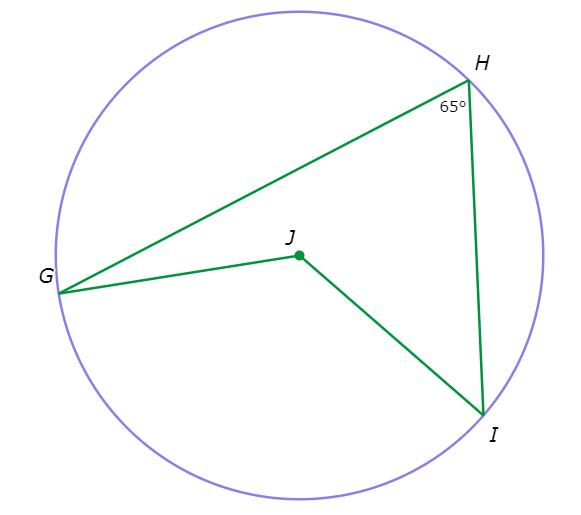
∠J=______ °

Look at the diagram:

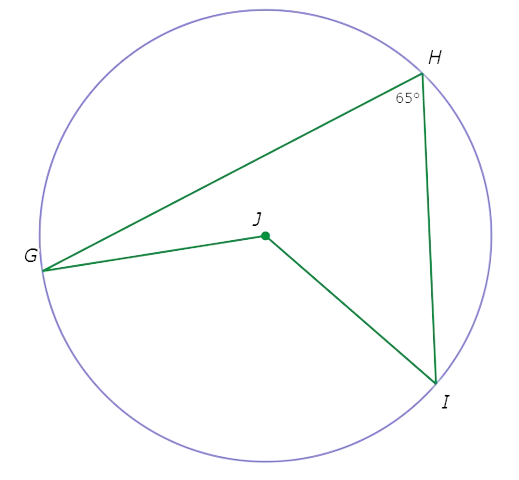
∠GHI is an inscribed angle that intercepts the same arc as the central angle ∠J, so use the Inscribed Angle Theorem.
∠J = 2 . ∠GHI Inscribed Angle Theorem
= 2 . (65°) Plug in ∠GHI=65°
= 130° Multiply
∠J is 130°.

let’s practice!