Circle measurements: mixed review
Key Notes :
๐ต Parts of a Circle
- Radius (r) โ Distance from center to any point on the circle.
- Diameter (d) โ Twice the radius ( d = 2r ).
- Circumference โ The distance around the circle.
- Chord โ A line segment joining two points on the circle.
- Arc โ A part of the circumference.
- Sector โ A “pizza slice ๐” shaped region.
๐ Circumference Formulas
- Using radius:
๐ C = 2ฯr - Using diameter:
๐ C = ฯd
๐ Area of a Circle
- Formula:
๐ A = ฯrยฒ - Remember: Square the radius first! ๐ง โจ
๐ข Arc Length (L)
- For an arc with central angle ฮธ (in degrees):
๐ L = (ฮธ / 360ยฐ) ร Circumference - Part of the circle = part of the circumference! ๐
๐ Area of a Sector
- Formula:
๐ Areaโโcโโแตฃ = (ฮธ / 360ยฐ) ร ฯrยฒ - Itโs like taking a slice of the full circleโs area. ๐ฅง
๐บ Relationship Between Radius & Diameter
- If radius is known โ find diameter: d = 2r
- If diameter is known โ find radius: r = d รท 2
๐ Using ฯ Values
- For simple questions: use ฯ = 22/7
- For accuracy: use ฯ = 3.14 or leave answer in ฯ form.
- Example: 14ฯ cm โ๏ธ is acceptable.
๐งฎ Mixed Review Tips
- Identify what is given: r? d? ฮธ?
- Choose the correct formula.
- Check if the angle is a fraction of the circle.
- Keep units consistent (cmยฒ for area, cm for circumference).
๐ Real-Life Applications
- Designing wheels ๐ฒ
- Circular tracks ๐โโ๏ธ
- Pizza slices ๐
- Clock faces ๐
Learn with an example
The diameter of a circle is 16 centimetres. What is the angle measure of an arc bounding a sector with area 8โ๐ square centimetres?
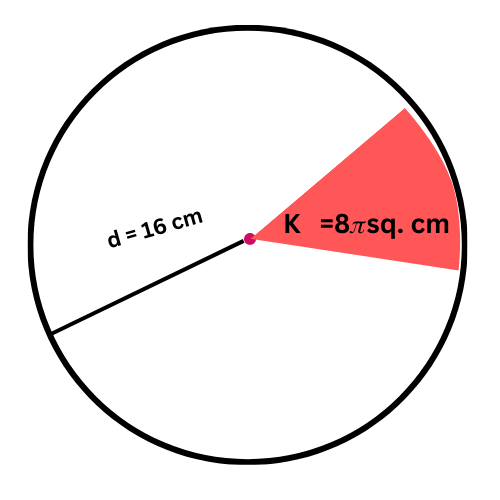
Give the exact answer in simplest form.
________ยฐ
The arc’s measure can be found from the sector’s area and the circle’s area. You already know that the sector’s area is 8โ๐square centimetres, so find the circle’s area.
To find the area, first find the radius.
d = 2r
16 = 2r Plug in d=16
8 = r Divide both sides by 2
The radius is 8 centimetres.
Next, find the area of the circle.
A = โ๐r2
= โ๐ . 82 Plug in r=8
= 64 โ๐ Square
The area of the circle is 64โ๐ square centimetres.
Finally, find the angle measure of the arc.
K = A . m/360
8โ๐ = 64 ๐ m/ 360 Plug in K=8โ๐ and A=64๐
8โ๐ . 360 / 64 ๐ =m Multiply both sides by 360 / 64 ๐
45 = m Multiply and simplify
The angle measure of the arc is 45ยฐ.
The Radius of a circle is 7 metres . what is the area ?
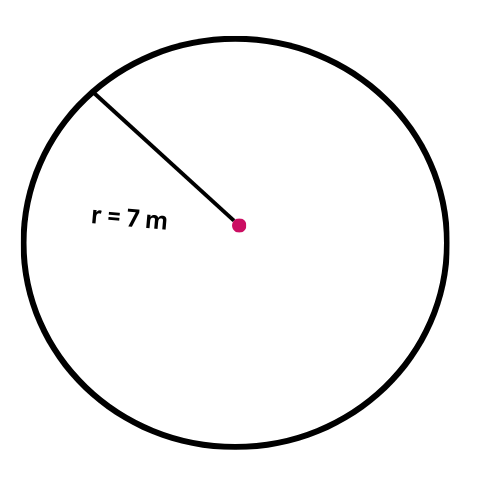
Give the exact answer in simplest form.
_______ square metres
Find the area.
A = โ๐r2
= โ๐.72 Plug in r=7
= 49โ๐ Square
The area is 49โ๐ square metres.
The circumference of a circle is 4โ๐ metres. What is the area?
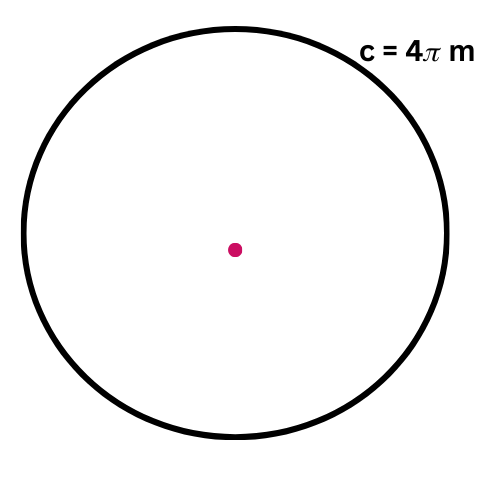
Give the exact answer in simplest form.
_______ square metres
First, find the radius.
C = 2๐r
4๐ = 2๐r Plug in C=4โ๐
2 = r Divide both sides by 2โ๐
The radius is 2 metres.
Now, find the area.
A = โ๐r2
= โ๐.22 Plug in r=2
= 4 โ๐ Square
The area is 4โ๐ square metres.
Let’s practice!
