Area of sectors
Key Notes :
🔵 What is a Sector?
A sector is a part of a circle that looks like a slice of pizza 🍕 or a piece of pie 🥧.
🔶 Formula for Area of a Sector
If a circle has radius r and the central angle is θ (in degrees):
👉 Area of a sector = (θ / 360°) × πr²
🟣 This formula tells us what fraction of the circle the sector represents.
🟩 When Angle is in Radians
If angle is θ radians:
👉 Area = (1/2) × r² × θ
📏 Radians are often used in higher classes, but good to know!
🟠 Understanding the Formula
- Full circle = 360°
- Sector = part of the circle
So multiply fraction of circle × area of full circle.
💛 Important Terms
- Radius (r) ➝ distance from center to edge of circle
- Central Angle (θ) ➝ angle that opens the sector
- π (pi) ➝ approximately 3.14
🟣 Area Depends On:
✔ Size of angle (θ) ➝ Bigger angle = bigger sector
✔ Size of radius (r) ➝ Larger circle = larger sector
💙 Real-Life Examples of Sectors
🍕 Pizza slices
🕗 Clock face sections
🎡 Ferris wheel sections
⚙ Machine gears
🧠 Sample Quick Example
Find the area of a sector with
- r = 7 cm
- θ = 60°
👉 Area = (60/360) × π × 7²
👉 Area = (1/6) × π × 49
👉 Area = (49π / 6) cm² 🎉
🌈 Tips for Solving Problems
⭐ Convert angle to degrees or radians correctly
⭐ Always write formula first
⭐ Square the radius carefully
⭐ Simplify fractions before multiplying for ease
Learn with an example
The radius of a circle is 10 centimetres. What is the area of a sector bounded by a 180° arc?
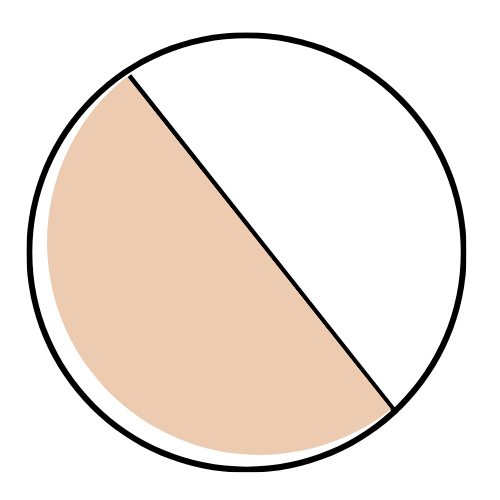
Give the exact answer in simplest form.
___________ square centimetres
The sector’s area depends on the arc’s measure and the circle’s area. You already know that the arc’s measure is 180°, so find the circle’s area.
First, find the area of the circle.
A = 𝜋 r2
= 𝜋 102 Plug in r=10
= 100 𝜋 Square
The area of the circle is 100𝜋 square centimetres.
Now, find the area of the sector.
K = A . m/360
= 100 𝜋 180 / 360 Plug in A=100𝜋 and m=180
= 50 𝜋 Multiply and simplify
The area of the sector is 50𝜋 square centimetres.
The radius of a circle is 8 kilometres. What is the area of a sector bounded by a 45° arc?
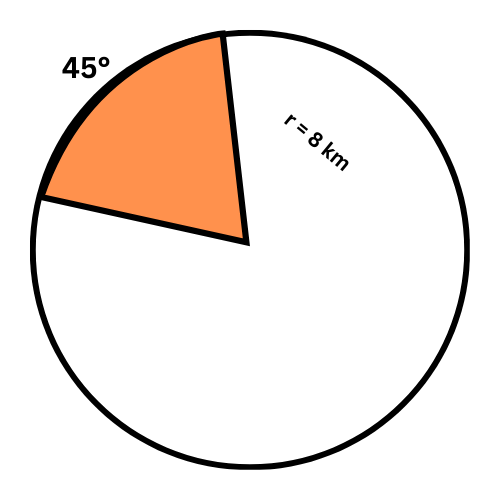
Give the exact answer in simplest form.
_________ square kilometres
The sector’s area depends on the arc’s measure and the circle’s area. You already know that the arc’s measure is 45°, so find the circle’s area.
First, find the area of the circle.
A = 𝜋 r2
= 𝜋 82 Plug in r=8
= 64 𝜋 Square
The area of the circle is 64𝜋 square kilometres.
Now, find the area of the sector.
K = A . m/360
= 64 𝜋 45 / 360 Plug in A=64𝜋 and m=45
= 8 𝜋 Multiply and simplify
The area of the sector is 8𝜋 square kilometres.
The radius of a circle is 6 centimetres. What is the area of a sector bounded by a 90° arc?
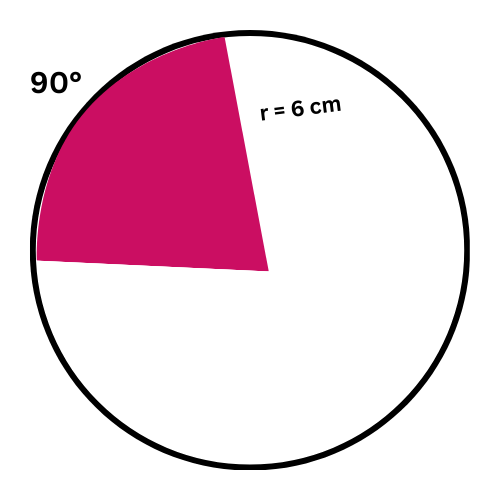
Give the exact answer in simplest form.
___________ square centimetres
The sector’s area depends on the arc’s measure and the circle’s area. You already know that the arc’s measure is 90°, so find the circle’s area.
First, find the area of the circle.
A = 𝜋 r2
= 𝜋 62 Plug in r=6
= 36 𝜋 Square
The area of the circle is 36𝜋 square centimetres.
Now, find the area of the sector.
K = A . m/360
= 36 𝜋 90 / 360 Plug in A=36 𝜋 and m=90
= 9 𝜋 Multiply and simplify
The area of the sector is 9𝜋 square centimetres.
Let’s practice!

