Arc measure and arc length
Key Notes :
π΅ What is an Arc?
An arc is a part of the circumference of a circle.
It looks like a curved segment of the circle.
Two types:
- Minor Arc β smaller than half the circle
- Major Arc β larger than half the circle
π’ Arc Measure (in degrees) π―
- Arc measure is the degree measure of the central angle that forms the arc.
- A full circle = 360Β°
- Minor arcs: measure < 180Β°
- Major arcs: measure > 180Β°
- Example: If central angle = 60Β°, then arc measure = 60Β° π
π£ Arc Length (actual distance) π
Arc length tells how long the curved part is (in cm, m, etc.).
β¨ Formula for Arc Length:
ArcΒ Length = ΞΈ / 360β Γ 2Οr
Where:
- ΞΈ = arc measure (in degrees)
- r = radius of the circle
π Example:
If r = 7βcm and ΞΈ = 90β
ArcΒ Length = 90 / 360 Γ 2Ο(7) = 14Ο = 3.5ΟΒ cm
π‘ Relationship between Arc Measure & Length
- Arc measure = tells βhow big the angle isβ (in Β°)
- Arc length = tells βhow long the curved path isβ (in cm/m)
- Bigger angle = longer arc
π΄ Special Case: Semicircle
- A semicircle = half the circle
- Arc measure = 180Β°
- Arc length = Β½ Γ circumference = Οr\pi rΟr
π Tips to Remember
- Use degrees for arc measure.
- Use radius for arc length.
- Always check if angle is minor or major.
- For full circle: arc length = 2Οr π
Learn with an example
π The radius of a circle is 3 metres. What is the length of a 90Β° arc?
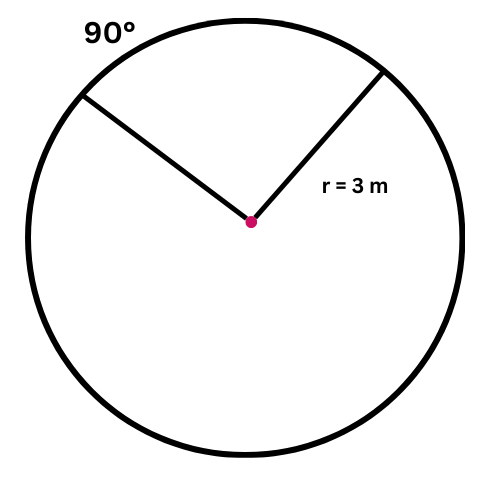
Give the exact answer in simplest form.
________ metres
The arc’s length depends on the arc’s measure and the circle’s circumference. You already know that the arc’s measure is 90Β°, so find the circle’s circumference.
First, find the circumference.
C = 2βπr
= 2βπ(3) Plug in r=3
= 6βπ Multiply
The circumference is 6βπ metres.
Now, find the length of the arc.
π = C . m / 360
= 6βπ . 90 / 360 Plug in C=6βπ and m=90
= 3βπ / 2 Multiply and simplify
The length of the arc is 3βπ / 2 metres
π The radius of a circle is 5 kilometres. What is the length of a 135Β° arc?
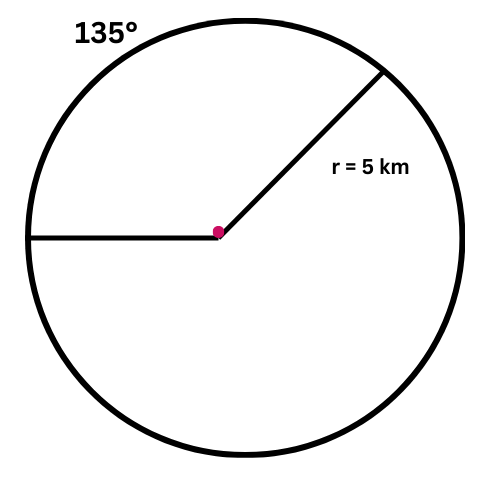
Give the exact answer in simplest form.
________ kilometres
The arc’s length depends on the arc’s measure and the circle’s circumference. You already know that the arc’s measure is 135Β°, so find the circle’s circumference.
First, find the circumference.
C = 2βπr
= 2βπ(5) Plug in r=5
= 10βπ Multiply
The circumference is 10βπ kilometres.
Now, find the length of the arc.
π=C . m / 360
= 10βπ . 135 / 360 Plug in C=10βπ and m=135
= 15π / 4 Multiply and simplify
The length of the arc is 15π / 4 kilometres.
π The radius of a circle is 10 centimetres. What is the length of a 135Β° arc?
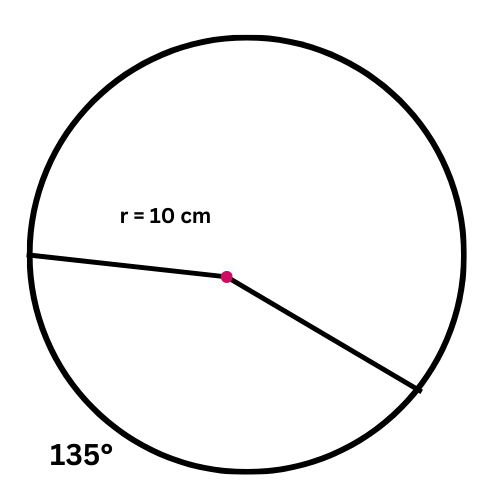
Give the exact answer in simplest form.
________ centimetres
The arc’s length depends on the arc’s measure and the circle’s circumference. You already know that the arc’s measure is 135Β°, so find the circle’s circumference.
First, find the circumference.
C = 2βπr
= 2βπ(10) Plug in r=10
= 20βπ Multiply
The circumference is 20βπ centimetres.
Now, find the length of the arc.
π = C . m / 360
=20βπ . 135 / 360 Plug in C=20βπ and m=135
= 15βπ / 2 Multiply and simplify
The length of the arc is 15βπ / 2 centimetres.
Let’s practice!
