Angles in inscribed quadrilaterals
Key Notes :
🔵 What is an Inscribed Quadrilateral?
- An inscribed quadrilateral is a four-sided shape where all vertices (corners) lie on a single circle — this circle is called the circumscribed circle.
- Each side acts like a chord of the circle.
📌Key Theorems and Properties
✅ Property 1: Opposite Angles are Supplementary
- In an inscribed quadrilateral, the opposite angles add up to 180° (they are supplementary).
∠A + ∠C = 180∘ and ∠B + ∠D = 180∘
✅ Property 2: Exterior Angle Rule
- An exterior angle of an inscribed quadrilateral equals the interior opposite angle.
∠E = ∠C
(where E is an exterior angle at vertex B opposite angle C)
✅ Property 3: Cyclic Quadrilateral Condition
- A quadrilateral can only be inscribed in a circle if its opposite angles are supplementary.
- If you check this property and it holds true, you confirm the quadrilateral is cyclic.
🛠️Example Problem
✅ Example 1:
If an inscribed quadrilateral has angles ∠A = 80∘ and ∠C = 100∘, find ∠B and ∠D.
👉 Solution:
- Opposite angles are supplementary:
∠A + ∠C = 180∘ ⟹ 80∘+100∘ = 180∘✅ Correct
For the other pair:
∠B + ∠D = 180∘
If ∠B = 110∘, then:
∠D = 180∘ − 110∘ = 70∘
👉 Final Answer: ∠B = 110∘ , D = 70∘
🔥Common Mistakes to Avoid
⚠️ 1. Confusing adjacent angles with opposite angles — Only opposite angles are supplementary, not adjacent ones.
⚠️ 2. Forgetting the exterior angle rule — Exterior angles are equal to the interior opposite angle, not adjacent angles.
⚠️ 3. Assuming all quadrilaterals are cyclic — A quadrilateral is only cyclic if the opposite angles are supplementary.
🧠Real-Life Applications
- Architecture: Circular windows with decorative inscribed designs.
- Engineering: Gear and wheel designs in machines.
- Astronomy: Calculating angles in planetary orbits.
Learn with an example
➡️ What is ∠D?
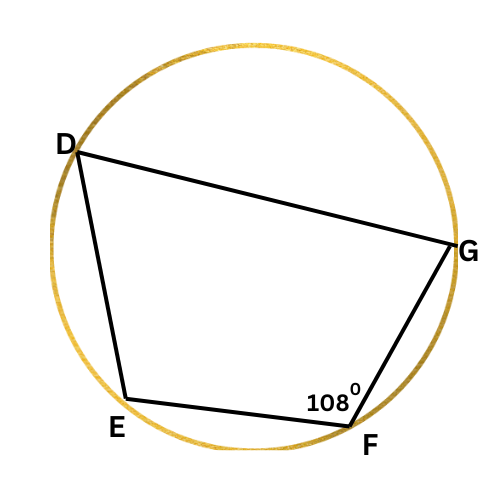
∠D=_____ °
Look at the diagram:
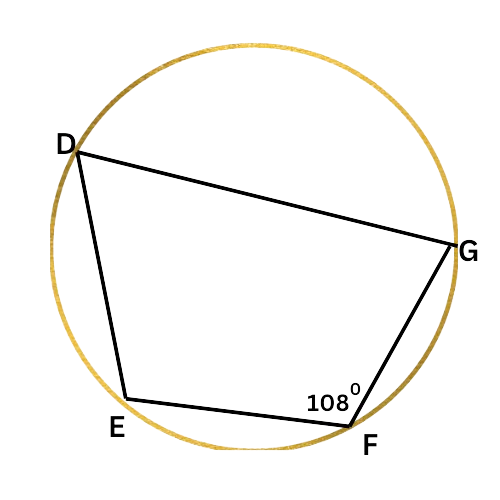
Since DEFG is an inscribed quadrilateral, ∠F and ∠D are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠D.
∠F+∠D=180°
108°+∠D=180° Plug in ∠F=108°
∠D=72° Subtract 108° from both sides
∠D is 72°.
➡️ What is ∠H?
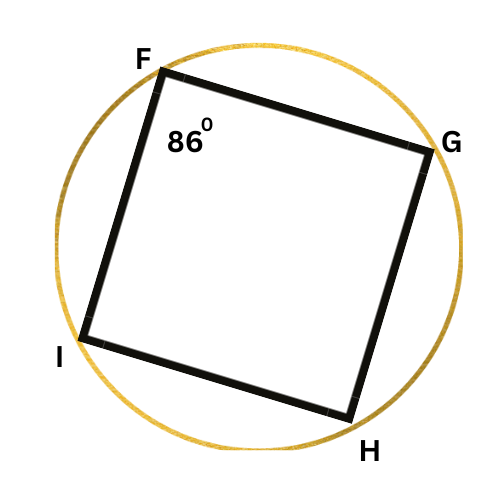
∠H=______ °
Look at the diagram:
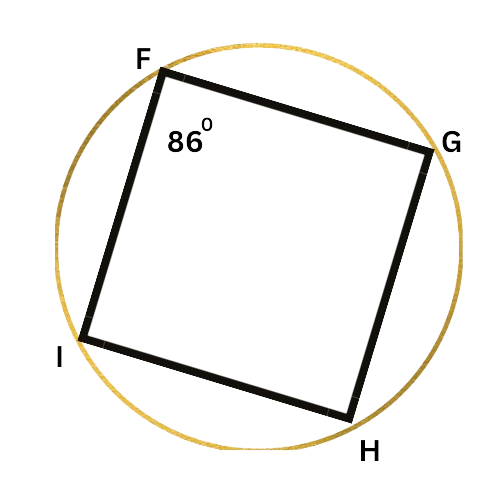
Since FGHI is an inscribed quadrilateral, ∠F and ∠H are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠H.
∠F+∠H=180°
86°+∠H=180° Plug in ∠F=86°
∠H=94° Subtract 86° from both sides
∠H is 94°.
➡️ What is ∠G?
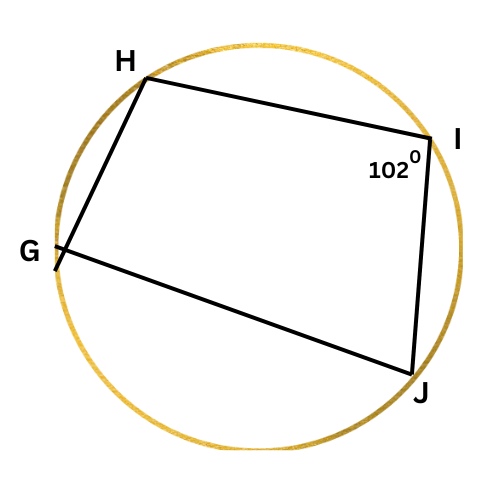
∠G=________ °
Look at the diagram:
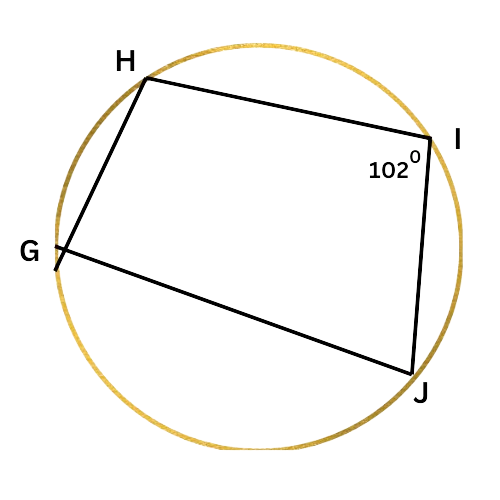
Since GHIJ is an inscribed quadrilateral, ∠I and ∠G are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠G.
∠I+∠G=180°
102°+∠G=180° Plug in ∠I=102°
∠G=78° Subtract 102° from both sides
∠G is 78°.
let’s practice!

