Angles in inscribed right triangles
Key Notes :
If AC is a diameter of a circle, then the inscribed angle ∠ABC is a right angle.
Learn with an example
🔔 What is ∠K?
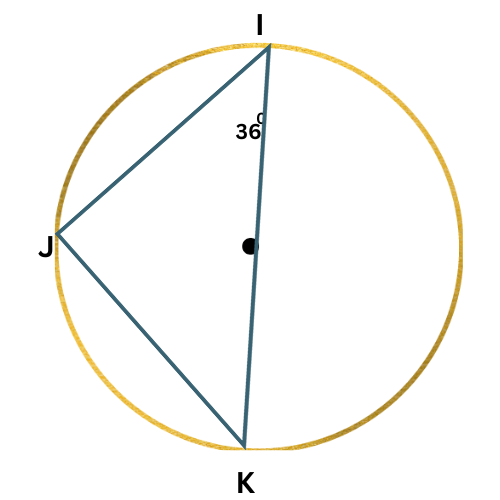
∠K=______ °
Since IK is a diameter of the circle, ∠J is a right angle.
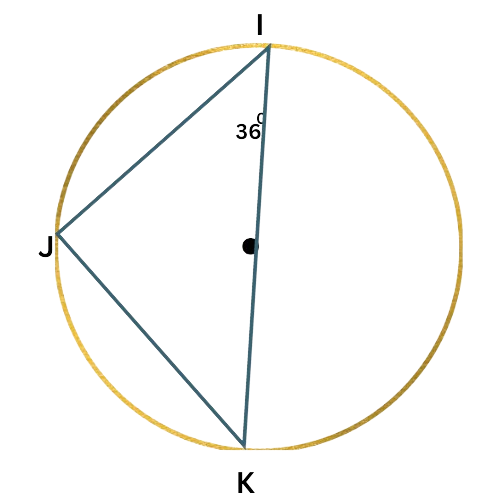
So, △IJK is a right triangle and ∠I and ∠K are complementary. Write an equation setting the sum of their measures equal to 90°, and solve for ∠K.
∠I+∠K=90°
36°+∠K=90° Plug in ∠I=36°
∠K=54° Subtract 36° from both sides
∠K is 54°.
🔔 What is ∠F?
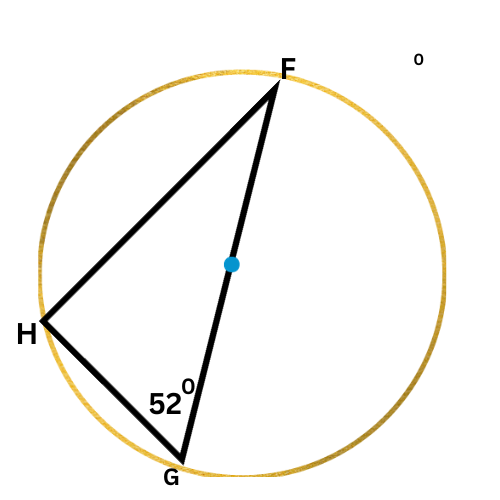
∠F=_______ °
Since FG is a diameter of the circle, ∠H is a right angle.
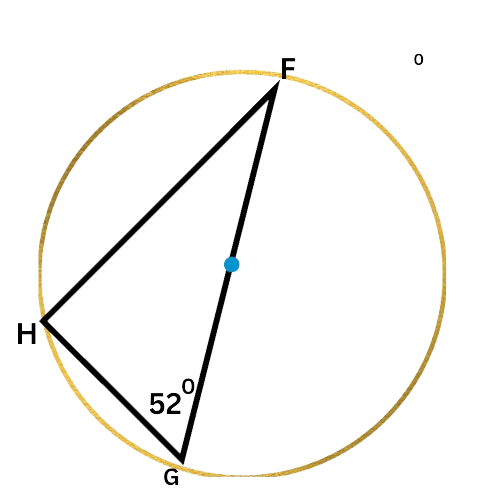
So, △FGH is a right triangle and ∠G and ∠F are complementary. Write an equation setting the sum of their measures equal to 90°, and solve for ∠F.
∠G+∠F=90°
52°+∠F=90° Plug in ∠G=52°
∠F=38° Subtract 52° from both sides
∠F is 38°.
🔔 What is ∠H?
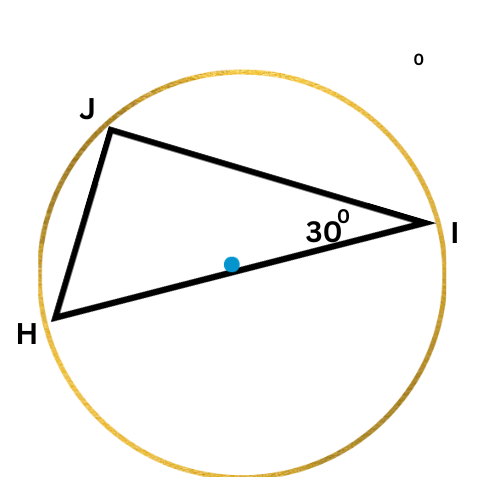
∠H=______ °
Since HI is a diameter of the circle, ∠J is a right angle.
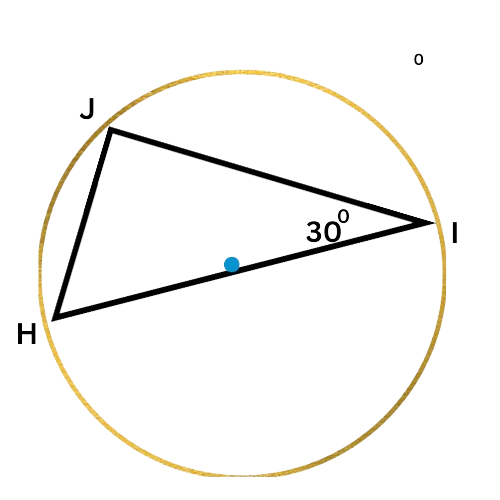
So, △HIJ is a right triangle and ∠I and ∠H are complementary. Write an equation setting the sum of their measures equal to 90°, and solve for ∠H.
∠I+∠H=90°
30°+∠H=90° Plug in ∠I=30°
∠H=60° Subtract 30° from both sides
∠H is 60°.
let’s practice!
