Review: properties of quadrilaterals
key notes :
🔹 Quadrilaterals – Overview
- A quadrilateral is a polygon with 4 sides and 4 angles. 🟦
- Sum of interior angles: 360° ➕
- Can be convex (all angles < 180°) or concave (one angle > 180°). 🔺
🔹 Types of Quadrilaterals & Properties
1️⃣ Square ⬜
- All sides equal ➖
- All angles 90° ➕
- Opposite sides are parallel ↔️
- Diagonals are equal & bisect at 90° ✖️
2️⃣ Rectangle ▭
- Opposite sides equal & parallel ↔️
- All angles 90° ➕
- Diagonals are equal but do not bisect at 90° ✖️
3️⃣ Rhombus ♦️
- All sides equal ➖
- Opposite angles are equal ↔️
- Diagonals bisect each other at 90° ✖️
- Diagonals not equal ❌
4️⃣ Parallelogram ▱
- Opposite sides equal & parallel ↔️
- Opposite angles are equal ↔️
- Diagonals bisect each other but not necessarily equal ✖️
5️⃣ Trapezium / Trapezoid 🔺
- Only one pair of opposite sides parallel ↔️
- Non-parallel sides are called legs
- Angles adjacent to the same leg are supplementary ➕
6️⃣ Kite 🪁
- Two pairs of adjacent sides equal ➖
- One pair of opposite angles equal ↔️
- Diagonals perpendicular ✖️
- One diagonal bisects the other
🔹 Quick Tips 💡
- Diagonals: Check if they are equal or perpendicular. ✖️
- Angles: Check if all 90° or opposite angles equal. 🔄
- Sides: Look for equal sides or parallel sides ↔️
Learn with an example
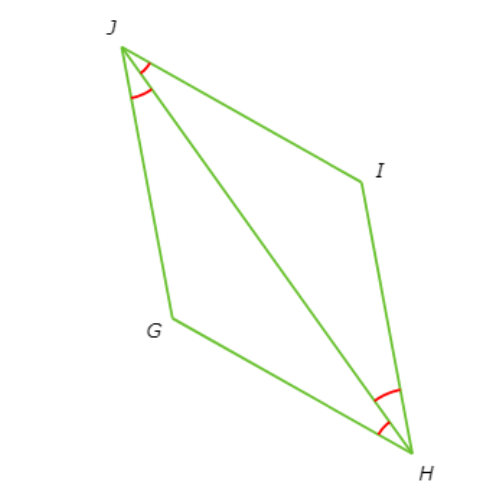
Is parallelogram GHIJ a rhombus?
- yes
- no
Since ∠GHJ ≅ ∠GJH ≅ ∠HJI ≅ ∠IHJ, HJ bisects ∠GHI and ∠GJI.
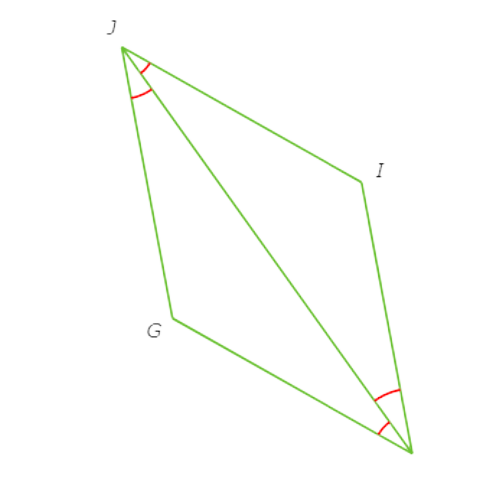
So, GHIJ is a rhombus.
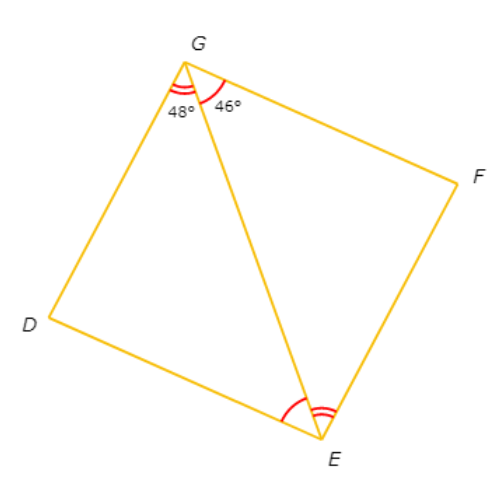
Is parallelogram DEFG a rhombus?
- yes
- no
Since ∠EG F= ∠DEG = 46° and ∠DGE = ∠FEG = 48°, EG does not bisect ∠DGF and ∠DEF.
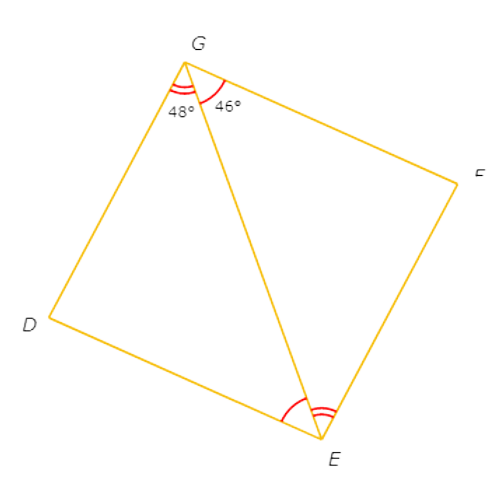
So, DEFG is not a rhombus.
Is parallelogram WXYZ a rhombus?

- yes
- no
Since ∠YVZ = 88°, WY and XZ are not perpendicular.
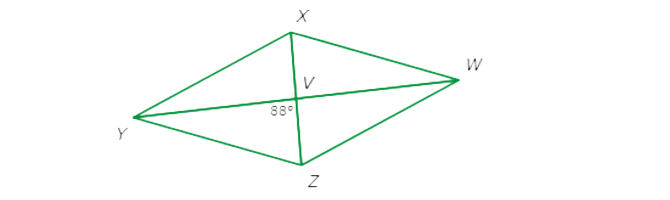
So, WXYZ is not a rhombus.
Let’s practice!

