Properties of kites
key notes :
🌟 Properties of Kites 🌟
Definition of a Kite ✈️
A kite is a quadrilateral with two distinct pairs of adjacent sides equal.
Example: If a kite has sides AB = AD and BC = CD, then it is a kite.
Diagonals ↕️↔️
The diagonals of a kite are perpendicular (meet at 90°) ⚡
One diagonal bisects the other (divides it into two equal parts). ✂️
Symmetry 🔷
A kite has one line of symmetry along the diagonal that bisects the other diagonal. 🪞
Angles 🔺
Angles between unequal sides are equal. ✅
Angles formed by the bisected diagonal are right angles (90°).
Area of a Kite 📐
Formula:
Area = 1/2 × d1 × d2
where d1 and d2 are the lengths of the diagonals.
Perimeter 🧮
Formula:
Perimeter = 2 × (sum of unequal sides)
Special Properties ✨
Two pairs of adjacent sides are equal. 💫
Exactly one diagonal bisects the other. 🪄
The longer diagonal bisects the angles at its ends. 🎯
💡 Tip for remembering:
Think of a kite flying in the sky: the stick (diagonal) is strong and straight, forming a cross with the tail 🪁.
Learn with an example
Quadrilateral HIJK is a kite. What is ∠J?
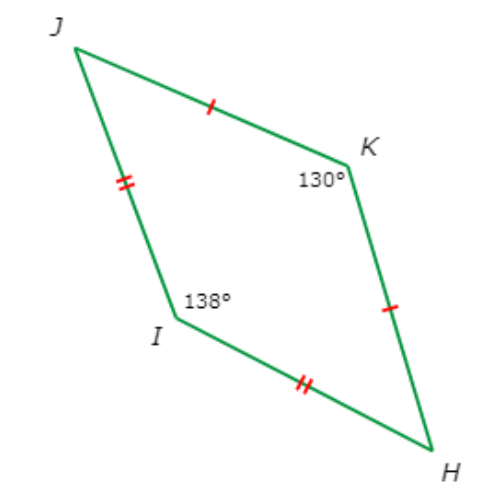
∠J= _____°
∠H and ∠J are opposite angles. Also, ∠I and ∠K are opposite angles.

Since HIJK is a kite and ∠I≠∠K, ∠H=∠J. Use the fact that the sum of the interior angle measures of a quadrilateral is 360° to set up an equation and solve for ∠J.
∠H + ∠I + ∠J + ∠K = 360°
∠J + ∠I + ∠J + ∠K = 360° Substitute ∠H = ∠J
2 . ∠J + ∠I + ∠K = 360° Combine like terms
2 . ∠J + 138° + 130° = 360° Plug in ∠I = 138° and ∠K = 130°
2 . ∠J + 268° = 360° Combine like terms
2 . ∠J = 92° Subtract 268° from both sides
∠J = 46° Divide both sides by 2
So, ∠J=46°.
Quadrilateral RSTU is a kite. What is ∠U?
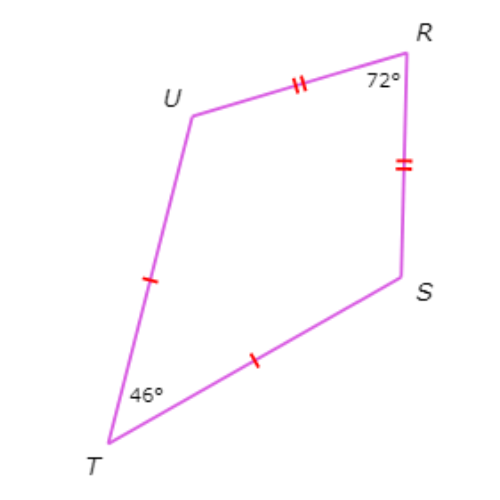
∠U= ____°
∠S and ∠U are opposite angles. Also, ∠R and ∠T are opposite angles.

Since RSTU is a kite and ∠R≠∠T, ∠S=∠U. Use the fact that the sum of the interior angle measures of a quadrilateral is 360° to set up an equation and solve for ∠U.
∠R+∠S+∠T+∠U = 360°
∠R+∠U+∠T+∠U = 360° Substitute ∠S=∠U
∠R+2∠U+∠T = 360° Combine like terms
72°+2∠U+46° = 360° Plug in ∠R=72° and ∠T=46°
2 . ∠U+118° = 360° Combine like terms
2 . ∠U = 242° Subtract 118° from both sides
∠U = 121° Divide both sides by 2
So, ∠U=121°.
| 🏋️♂️ Work it out🏋️♀️ Not feeling ready yet? These can help: 🥏Properties of parallelograms |
Let’s practice!

