Properties of trapeziums
key notes :
🟦 🔹 What is a Trapezium?
A trapezium (also called a trapezoid) is a quadrilateral with one pair of parallel sides.
👉 The parallel sides are called bases, and the non-parallel sides are called legs.
🟩 🔹 Basic Properties of a Trapezium
1️⃣ One Pair of Parallel Sides ➡️ Only one pair of opposite sides are parallel.
2️⃣ Sum of Interior Angles = 360° 🔄
3️⃣ Non-parallel sides (legs) can be equal or unequal in length.
4️⃣ The diagonals usually are not equal and don’t bisect each other (except in special types).
5️⃣ The line joining midpoints of the non-parallel sides is parallel to the bases and half the sum of the lengths of the bases. ➗
🧮 Formula:
👉 Mid-segment = ½ × (Base₁ + Base₂)
🟧 🔹 Types of Trapeziums
1️⃣ Isosceles Trapezium
✨ Non-parallel sides are equal in length.
✨ Base angles are equal.
✨ Diagonals are equal in length.
2️⃣ Right-Angled Trapezium
🟰 Has two right angles (90°).
📏 One leg is perpendicular to the bases.
🟥 🔹 Area and Perimeter Formulas
📐 Area (A) = ½ × (Sum of Parallel Sides) × (Height)
👉 A = ½ × (a + b) × h
📏 Perimeter (P) = Sum of all four sides
👉 P = a + b + c + d
🟪 🔹 Special Facts
💠 A parallelogram is not a trapezium because both pairs of sides are parallel.
💠 A square or rectangle cannot be a trapezium.
💠 Trapeziums are common in bridges, tables, and architectural designs 🏗️.
🌟 🔹 Fun Tip
Think of a trapezium as a “halfway shape” between a triangle and a parallelogram! ⏹️➡️🔺
Learn with an example
If UX is not parallel to VW , what is VW?
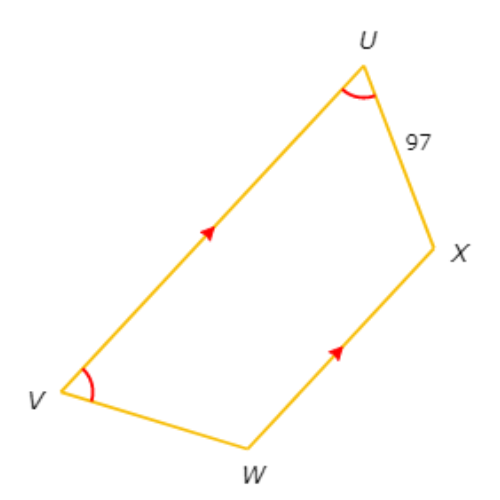
VW= ____
UVWX is a quadrilateral with exactly one pair of parallel sides, UV and WX , and one pair of congruent base angles, ∠U and ∠V.
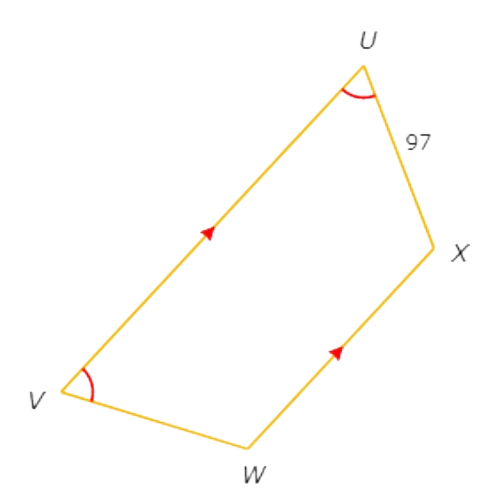
So, UVWX is an isosceles trapezium.
This means the legs are congruent. So, VW=UX=97.
If CD is not parallel to AB , what is CD?
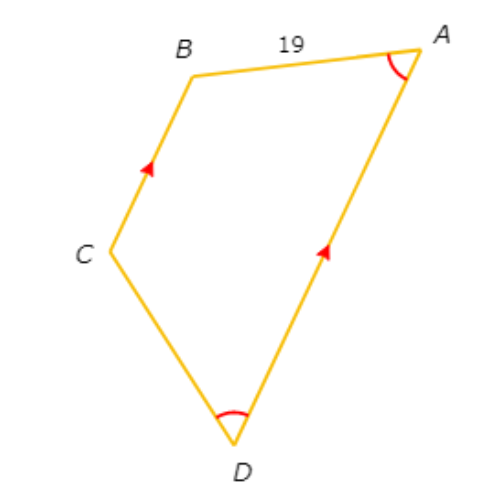
CD =_____
ABCD is a quadrilateral with exactly one pair of parallel sides, AD and BC , and one pair of congruent base angles, ∠D and ∠A.
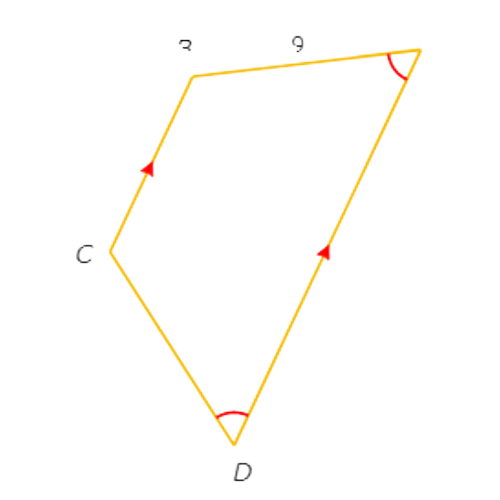
So, ABCD is an isosceles trapezium.
This means the legs are congruent. So, CD=AB=19.
If BE is not parallel to CD , what is BE?
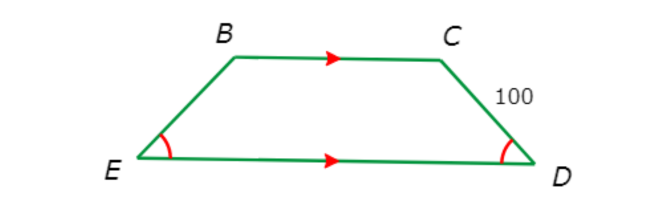
BE = ____
BCDE is a quadrilateral with exactly one pair of parallel sides, BC and DE , and one pair of congruent base angles, ∠E and ∠D.
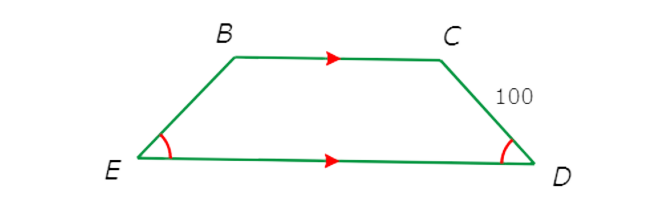
So, BCDE is an isosceles trapezium.
This means the legs are congruent. So, BE=CD=100.
Let’s practice!

