Properties of squares and rectangles

key notes :

Square

Definition: A square is a quadrilateral with all four sides equal and all angles 90°.

Properties:

  • All sides are of equal length.
  • All interior angles are 90°.
  • Opposite sides are parallel.
  • Diagonals are equal in length.
  • Diagonals bisect each other at right angles.
  • Diagonals bisect the angles at the vertices.
  • A square has rotational symmetry of order 4 and four lines of symmetry.

Area Formula: Area = side2

Perimeter Formula: Perimeter = 4 × side.

Rectangle

Definition: A rectangle is a quadrilateral with opposite sides equal and all angles 90°.

Properties:

  • Opposite sides are equal and parallel.
  • All interior angles are 90°.
  • Diagonals are equal in length.
  • Diagonals bisect each other but not necessarily at right angles.
  • A rectangle has rotational symmetry of order 2 and two lines of symmetry.

Area Formula: Area = length × width

Perimeter Formula: Perimeter = 2 × (length + width).

Comparison of Squares and Rectangles

  • A square is a specific type of rectangle where all sides are equal.
  • Both shapes have angles of 90°, but the square has diagonals that bisect at right angles, unlike the rectangle.
  • A square has more lines of symmetry (4) than a rectangle (2).

Learn with an example

Quadrilateral EFGH is a square. What is ∠DFE?

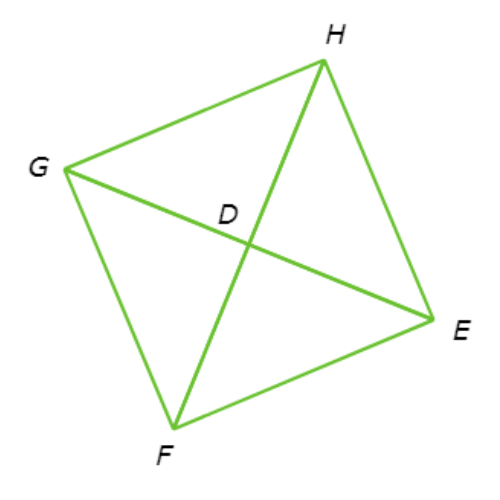
∠DFE= ____°

Since EFGH is a square, ∠EFG=90° and FH bisects ∠EFG.

So, ∠DFE=45°.

Quadrilateral TUVW is a square. What is ∠SWT?

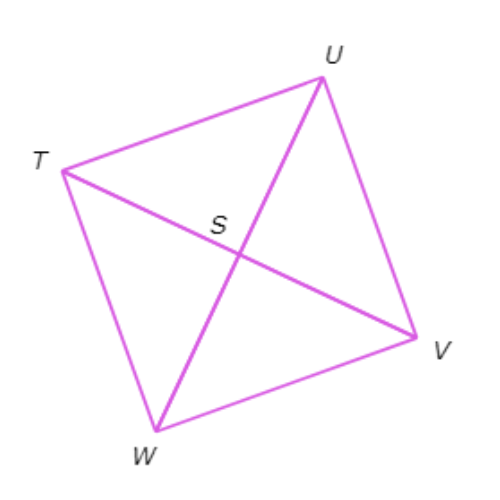
∠SWT= ____°

Since TUVW is a square, ∠TWV=90° and UW bisects ∠TWV.

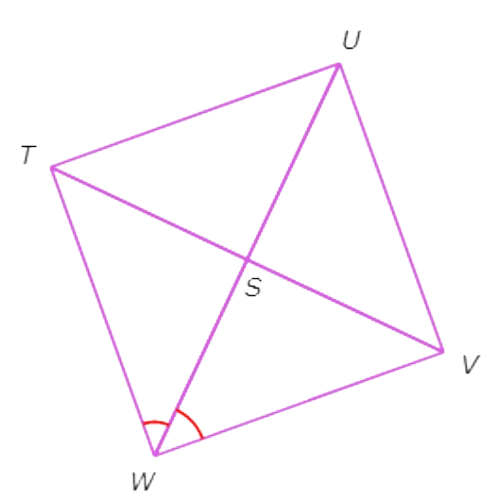
So, ∠SWT=45°.

Quadrilateral CDEF is a square. What is ∠EFG?

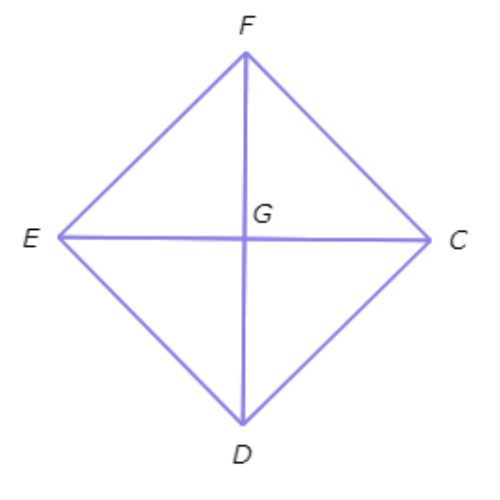
∠EFG= ____°

Since CDEF is a square, ∠CFE=90° and DF bisects ∠CFE.

So, ∠EFG=45°.

Let’s practice!