Proving a quadrilateral is a parallelogram
key notes :
🔹 Definition:
A parallelogram is a quadrilateral (4-sided figure) where both pairs of opposite sides are parallel. ➡️⬅️
📏 Ways to Prove a Quadrilateral is a Parallelogram:
There are five main methods to prove that a quadrilateral is a parallelogram 👇
🟩 Both pairs of opposite sides are parallel
➡️ AB ∥ CD and AD ∥ BC
✅ If both pairs of opposite sides are parallel, the quadrilateral is a parallelogram.
🧠 Example: If in quadrilateral ABCD, AB ∥ CD and AD ∥ BC → ABCD is a parallelogram.
🟨 Both pairs of opposite sides are equal
📏 AB = CD and AD = BC
✅ If both pairs of opposite sides are equal in length, it’s a parallelogram.
🧠 Example: If AB = CD and AD = BC → ABCD is a parallelogram.
🟦 One pair of opposite sides is both parallel and equal
➡️ AB ∥ CD and AB = CD
✅ If one pair of opposite sides is parallel and equal in length, the quadrilateral is a parallelogram.
🧠 Example: If AB ∥ CD and AB = CD → ABCD is a parallelogram.
🟧 Both pairs of opposite angles are equal
🔺 ∠A = ∠C and ∠B = ∠D
✅ If both pairs of opposite angles are equal, the quadrilateral is a parallelogram.
🧠 Example: If ∠A = ∠C and ∠B = ∠D → ABCD is a parallelogram.
🟥 The diagonals bisect each other
✂️ AC and BD bisect each other at midpoint O
✅ If the diagonals of a quadrilateral bisect each other, the figure is a parallelogram.
🧠 Example: If AO = OC and BO = OD → ABCD is a parallelogram.
💡 Remember:
- Every rectangle, rhombus, and square is a parallelogram because they all satisfy these conditions. 🧩
- Coordinate Geometry Tip: You can use the slope formula or distance formula to verify parallelism or equality. 📐
🧭 Quick Summary Table:
| Property | Condition | Result |
|---|---|---|
| 🔹 Opp. sides ∥ | Both pairs | Parallelogram |
| 🔸 Opp. sides = | Both pairs | Parallelogram |
| 🔺 1 pair ∥ & = | One pair | Parallelogram |
| 🔷 Opp. angles = | Both pairs | Parallelogram |
| ✂️ Diagonals bisect | Each other | Parallelogram |
🌈 Fun Fact:
All parallelograms are quadrilaterals, but not all quadrilaterals are parallelograms! 😉
Learn with an example
Can you show that this quadrilateral is a parallelogram?
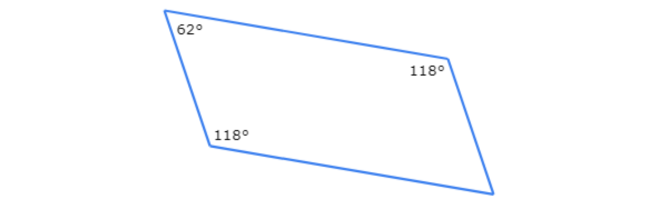
- yes
- no
One pair of opposite angles measures 118°. Another angle measures 62°.
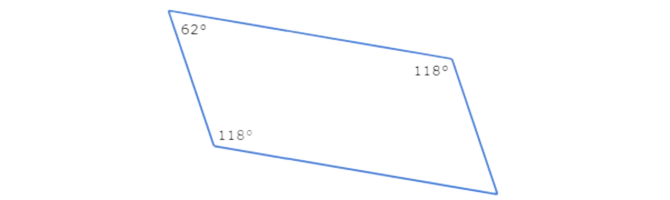
The quadrilateral is a parallelogram if the unlabeled angle also measures 62°. Call the unlabeled angle measure x. Set the sum of the interior angle measures equal to 360° and solve for x.
118°+62°+118°+x = 360°
298°+x = 360° Ad
x = 62° Subtract 298° from both sides
Since x=62°, both pairs of opposite angles are congruent. So, this quadrilateral is a parallelogram.
Can you show that this quadrilateral is a parallelogram?
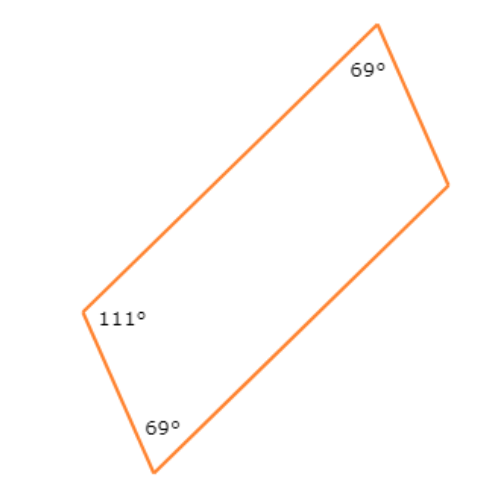
- yes
- no
One pair of opposite angles measures 69°. Another angle measures 111°.

The quadrilateral is a parallelogram if the unlabeled angle also measures 111°. Call the unlabeled angle measure x. Set the sum of the interior angle measures equal to 360° and solve for x.
69°+111°+69°+x = 360°
249°+x = 360° Add
x = 111° Subtract 249° from both sides
Since x=111°, both pairs of opposite angles are congruent. So, this quadrilateral is a parallelogram.
Can you show that this quadrilateral is a parallelogram?
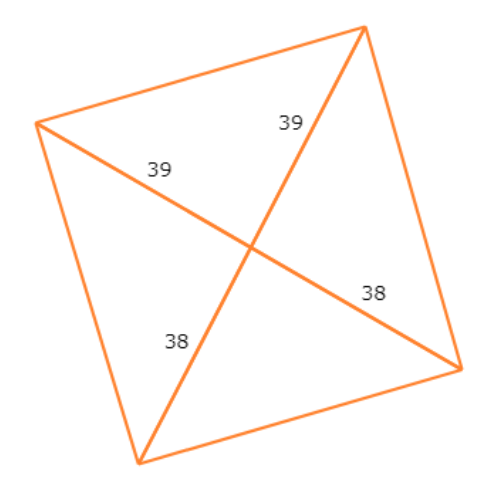
- yes
- no
Since one diagonal is split into non-congruent segments with length 39 and length 38, the diagonals do not bisect each other.

So, the quadrilateral is not a parallelogram.
| 🏋️♂️ Work it out🏋️♀️ Not feeling ready yet? These can help: 🥏Properties of parallelograms |
Let’s practice!

