Graph quadrilaterals
Key Notes:
🔹 What is a Quadrilateral?
👉 A quadrilateral is a polygon with 4 sides and 4 vertices (corners).
👉 The sum of all interior angles of a quadrilateral is 360°. 🔺➕🔻
🟪 Examples:
- Square ⬜
- Rectangle 🟦
- Parallelogram 🟩
- Rhombus 💎
- Trapezium ⏹️
🔹 Coordinate Plane Basics 🧭
👉 The coordinate plane has two axes:
- x-axis (horizontal)
- y-axis (vertical)
📍 Any point is represented as (x, y) — called an ordered pair.
🔹 Plotting the Vertices ✏️
👉 To graph a quadrilateral, plot all four vertices on the coordinate plane.
👉 Example:
Let the vertices be A(1,2), B(5,2), C(5,5), D(1,5).
📊 Plot them carefully on the grid and connect the points in order — it forms a rectangle! 🟦
🔹 Connecting the Points 🔗
🧩 After plotting, join the points in sequence — A→B→C→D→A — to form a closed figure.
💡 Make sure the figure starts and ends at the same point!
🔹 Checking the Type of Quadrilateral 🧮
You can determine the type of quadrilateral by using:
✅ Distance formula: to find side lengths
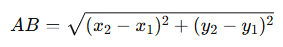
✅ Slope formula: to check if sides are parallel
m = y2 − y1 / x2 – x1
✅ Midpoint formula: to verify diagonals bisect each other
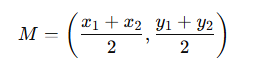
📏 Example: If opposite sides are equal and parallel, it’s a parallelogram! 🟩
🔹 Identify the Shape by Properties 🧠
| Quadrilateral | Properties |
|---|---|
| 🟦 Rectangle | Opposite sides equal & parallel; angles 90° |
| 💎 Rhombus | All sides equal; diagonals bisect at right angles |
| ⬜ Square | All sides equal; all angles 90° |
| ⏹️ Trapezium | Only one pair of opposite sides parallel |
🔹 Real-Life Applications 🌍
📐 Used in:
- Designing buildings and floors 🏠
- Computer graphics & animation 💻
- Map plotting and architecture 🗺️
🌟 Summary:
👉 Plot the points ➡️ Connect them ➡️ Identify the shape ➡️ Verify with formulas!
💪 Mastering graphing quadrilaterals helps in geometry, algebra, and real-world design. 🎨📈
Learn with an example
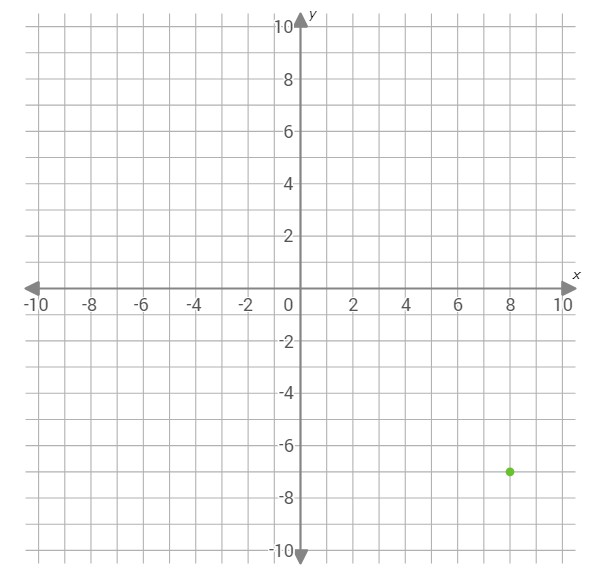
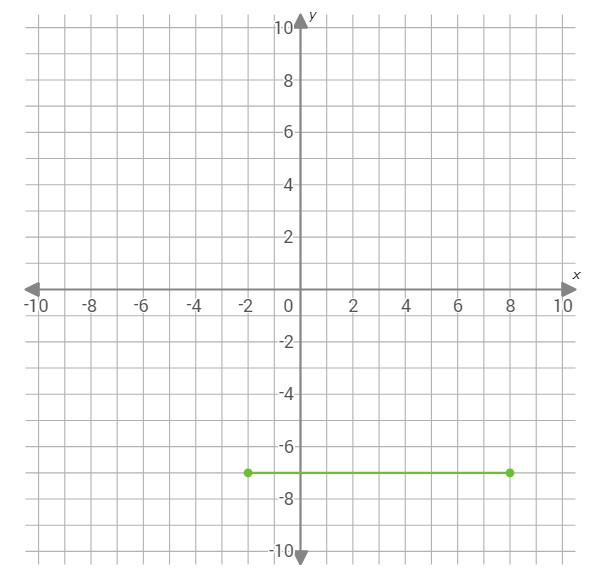
Graph the parallelogram with vertices (8,–7), (–2,–7), (0,5) and (10,5).
Graph the point (8,–7). Start at (0, 0). Move 8 units right and 7 units down.
To draw one side of the parallelogram, graph the point (–2,–7).
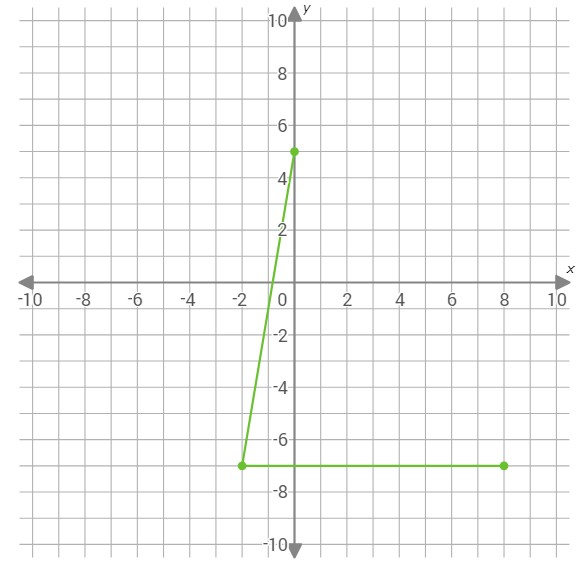
To draw another side of the parallelogram, graph the point (0,5).
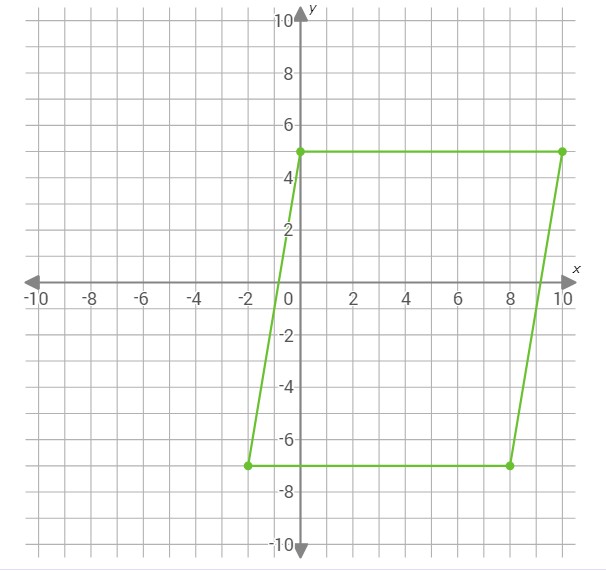
To complete the parallelogram, graph the point (10,5).
Graph the quadrilateral with vertices (–4,8), (–6,–3), (3,8) and (0,7).
Graph the point (4,8). Start at (0, 0). Move 4 units left and 8 units up.
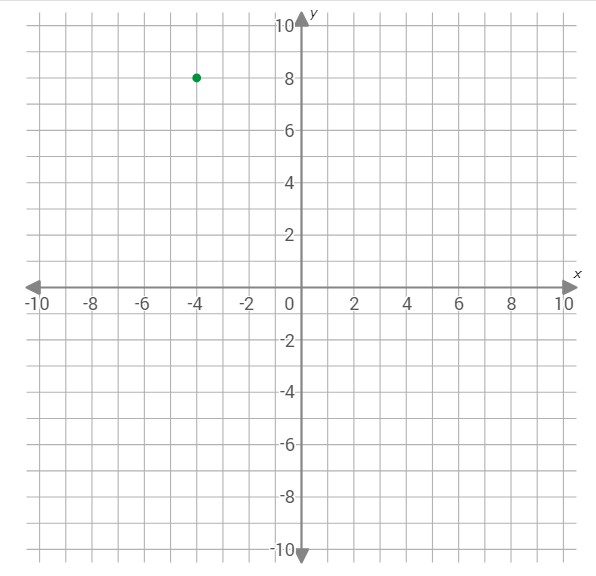
To draw one side of the quadrilateral, graph the point (–6,–3).
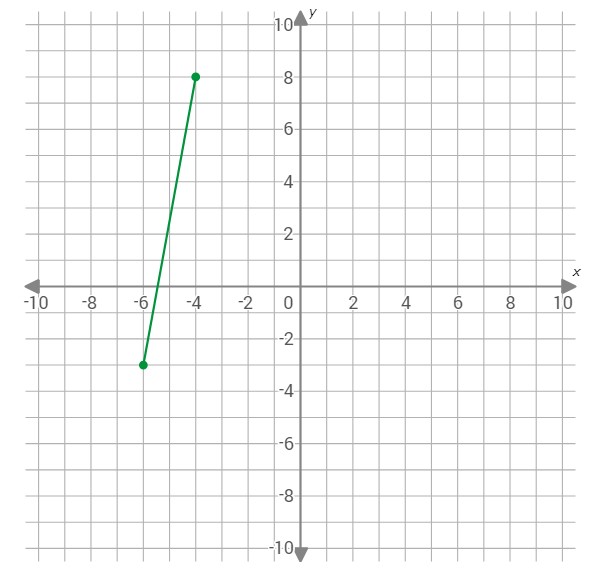
To draw another side of the quadrilateral, graph the point (3,8).
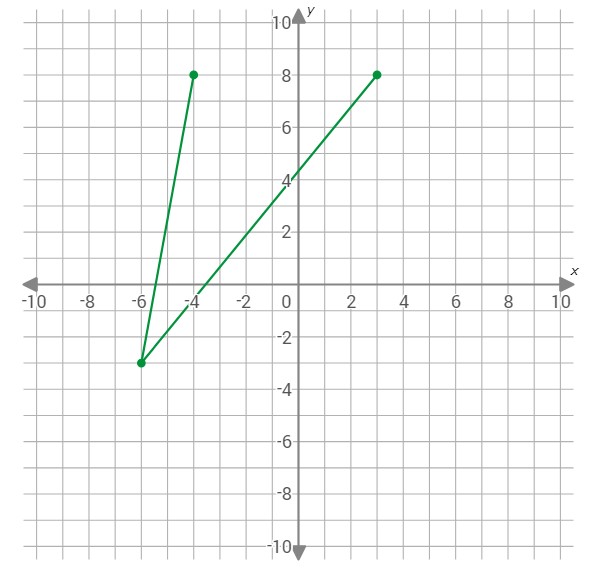
To complete the quadrilateral, graph the point (0,7).
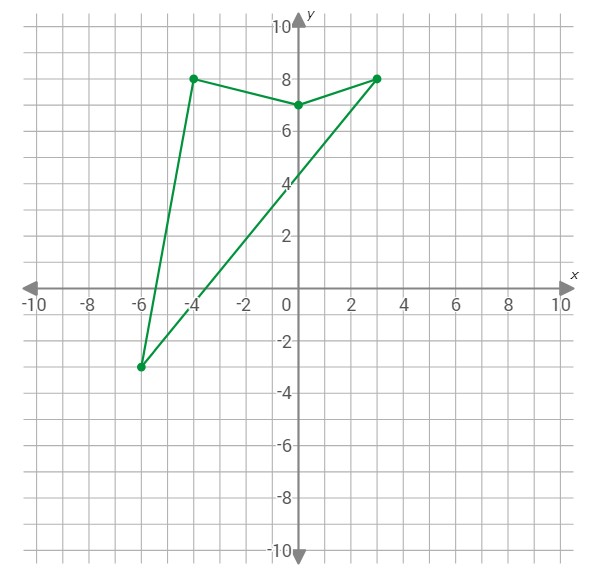
Let’s practice!

