Classify quadrilaterals
key notes :
🔷 💠 What is a Quadrilateral?
👉 A quadrilateral is a four-sided polygon.
It has:
- 🟢 4 sides
- 🔵 4 vertices (corners)
- 🟡 4 angles
- 🟥 The sum of interior angles is always 360°.
🟪 Types of Quadrilaterals
1️⃣ Parallelogram ♾️
➡️ Opposite sides are parallel and equal.
➡️ Opposite angles are equal.
➡️ Diagonals bisect each other.
🧠 Example: Rectangle, Rhombus, Square
2️⃣ Rectangle ⬜
✨ All angles are 90°.
✨ Opposite sides are equal and parallel.
✨ Diagonals are equal and bisect each other.
📏 Special Property: Every rectangle is a parallelogram.
3️⃣ Rhombus 💎
💠 All sides are equal.
💠 Opposite sides are parallel.
💠 Diagonals bisect each other at right angles (90°).
💠 Opposite angles are equal.
📏 Special Property: Every rhombus is a parallelogram.
4️⃣ Square 🟥
✅ All sides are equal.
✅ All angles are 90°.
✅ Diagonals are equal and bisect each other at right angles.
🌟 It’s both a rectangle and a rhombus!
5️⃣ Trapezium (Trapezoid) 🔻
⬆️ Only one pair of opposite sides is parallel.
📐 Special Types:
- Isosceles Trapezium – Non-parallel sides are equal & angles are equal.
- Right Trapezium – Has one right angle.
6️⃣ Kite 🪁
🎯 Two pairs of adjacent sides are equal.
🎯 One pair of opposite angles is equal.
🎯 Diagonals intersect at right angles, but do not bisect each other.
🧩 Properties Summary Table
| 🔹 Type | 🔸 Parallel Sides | 🔸 Equal Sides | 🔸 Equal Angles | 🔸 Diagonals Property |
|---|---|---|---|---|
| Parallelogram | 2 pairs | Opposite | Opposite | Bisect each other |
| Rectangle | 2 pairs | Opposite | All 90° | Equal & bisect |
| Rhombus | 2 pairs | All 4 | Opposite | Bisect at 90° |
| Square | 2 pairs | All 4 | All 90° | Equal & bisect at 90° |
| Trapezium | 1 pair | None | None | Unequal |
| Kite | None | Adjacent pairs | One pair | Intersect at 90° |
🌟 Fun Tip to Remember!
💡 “Some Rectangles Run Squarely Toward Kites”
(S → R → R → S → T → K) helps you recall Square, Rectangle, Rhombus, Square, Trapezium, Kite order!
🧠 In Short:
✅ All squares are rectangles,
✅ All rectangles and rhombuses are parallelograms,
✅ But not all parallelograms are rectangles or squares!
Learn with an example
What name best describes this polygon?
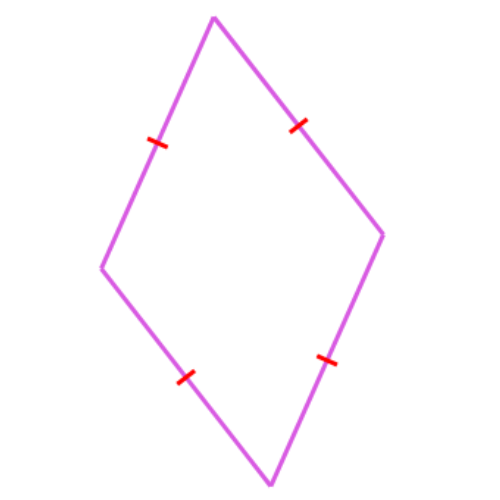
- square
- rectangle
- rhombus
- trapezium
Look at the polygon. Sides with matching hatch marks are congruent.
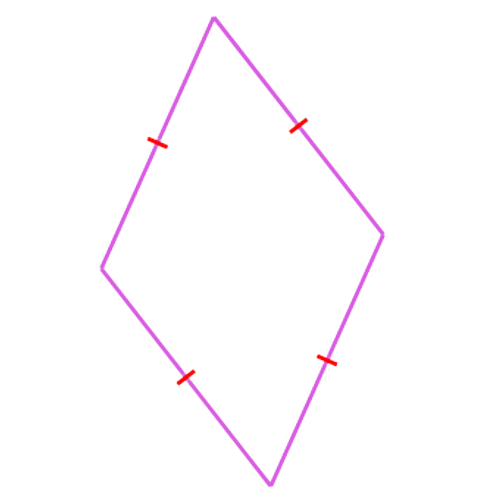
This polygon is best described as a rhombus.
What name best describes this polygon?
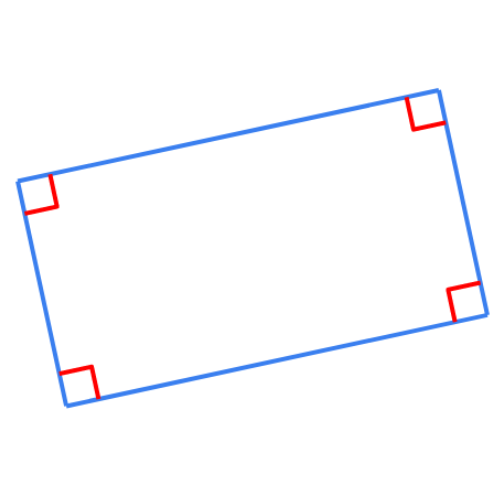
- parallelogram
- rectangle
- trapezium
- rhombus
Look at the polygon. All four angles are right angles.
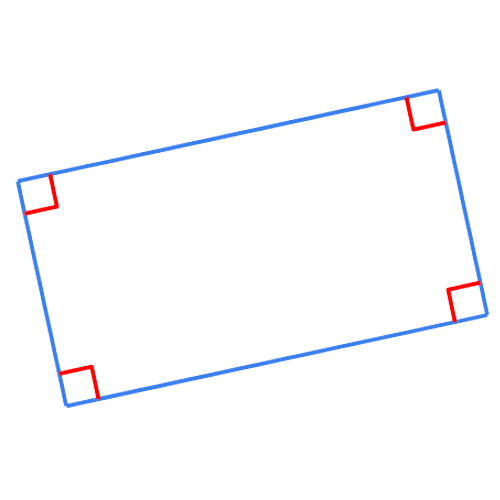
This polygon is best described as a rectangle.
What name best describes this polygon?
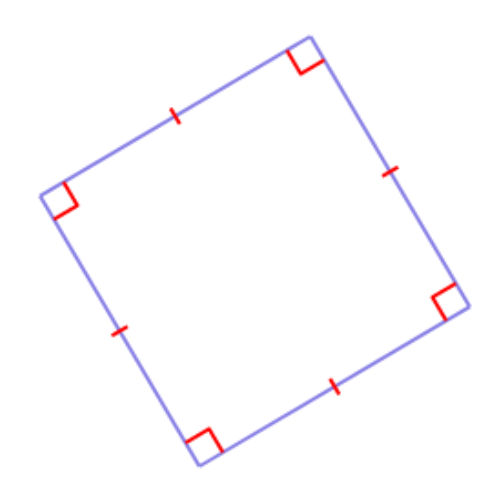
- square
- parallelogram
- trapezium
- rectangle
Look at the polygon. Sides with matching hatch marks are congruent.
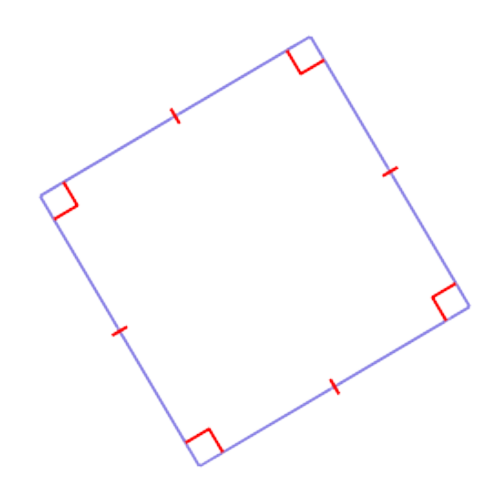
This polygon is best described as a square.
Let’s practice!

