SSS Theorem in the coordinate plane

key notes :

Definition of SSS Theorem

  • The Side-Side-Side (SSS) Congruence Theorem states that if three sides of one triangle are equal to three sides of another triangle, then the two triangles are congruent.

Using the Coordinate Plane

  • In a coordinate plane, the SSS theorem can be applied by using the distance formula to check if corresponding sides of two triangles are equal.
  • Distance formula:

d = (x2 − x1)2 + (y2 − y1)2

  • This formula helps determine the lengths of sides when given the coordinates of triangle vertices.

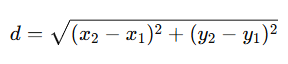
Steps to Prove Triangle Congruence Using SSS in the Coordinate Plane

  • Step 1: Identify the coordinates of the three vertices of both triangles.
  • Step 2: Use the distance formula to calculate the length of each side.
  • Step 3: Compare the corresponding side lengths of both triangles.
  • Step 4: If all three sides are equal, then the triangles are congruent by SSS Theorem.

Example Problem

Given two triangles:

  • Triangle A: A (1,2) , B (4,6) , C (7,2)
  • Triangle B: P (2,3) , Q (5,7) , R (8,3)

Find the distances AB, BC, AC and compare them with PQ, QR, PR to check for congruence.

Real-World Application

  • Used in navigation, engineering, and computer graphics to determine object placement and verify shapes.
  • Helps in map-making where distances between landmarks are analyzed for congruence.

Common Mistakes to Avoid

  • Incorrectly applying the distance formula.
  • Mixing up the coordinates when comparing sides.
  • Assuming angles are equal without verifying side lengths.

Learn with an example

Are △ABC and △XYZ congruent?

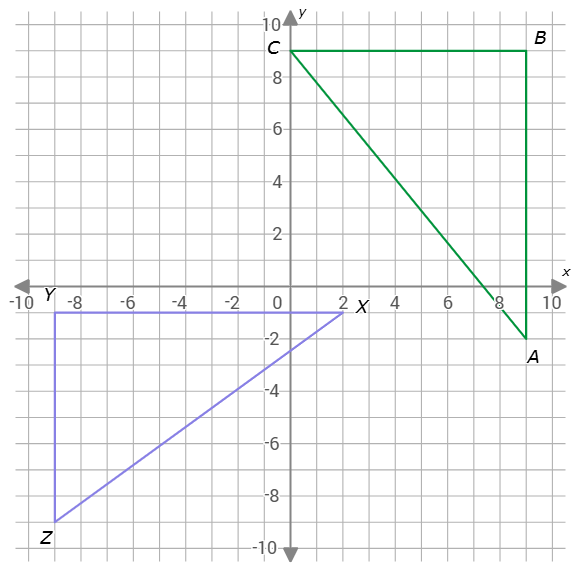
  • yes
  • no

To see that △ABC and △XYZ are not congruent, calculate the three side lengths of each triangle.

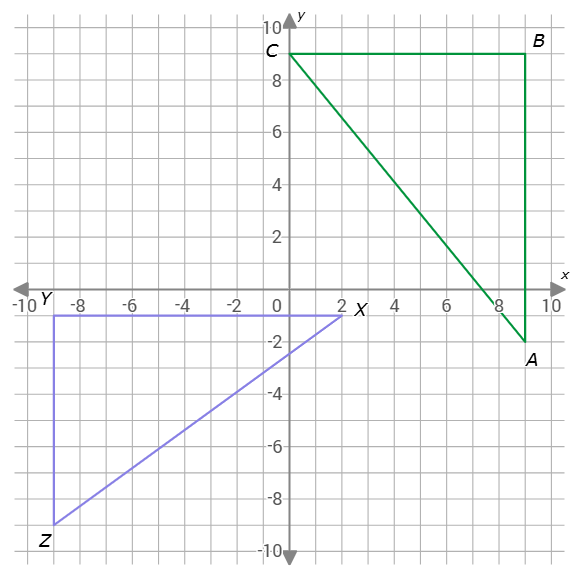
△ABC has vertices A(9,–2), B(9,9) and C(0,9) and △XYZ has vertices X(2,–1), Y(–9,–1) and Z(–9,–9).

Step 1: Find the side lengths of △ABC.

First, find AB. Since A(9,–2) and B(9,9) have the same x-coordinate, AB is the absolute value of the difference in the y-coordinates. So, AB=|9– –2|=11.

Second, find BC. Since B(9,9) and C(0,9) have the same y-coordinate, BC is the absolute value of the difference in the x-coordinates. So, BC=|0–9|=9.

Third, find AC. Since A(9,–2) and C(0,9) do not have equal x-coordinates or equal y-coordinates, use the distance formula to calculate AC. Plug in A(9,–2) for (x1,y1) and C(0,9) for (x2,y2), and simplify.

The three side lengths of △ABC are AB=11, BC=9, and AC=202.

Step 2: Find the side lengths of △XYZ.

First, find XY. Since X(2,–1) and Y(–9 , –1) have the same y-coordinate, XY is the absolute value of the difference in the x-coordinates. So, XY = |– 9 –2| = 11.

Second, find YZ. Since Y(–9,–1) and Z(–9,–9) have the same x-coordinate, YZ is the absolute value of the difference in the y-coordinates. So, YZ = | –9– –1| = 8.

Since no side of △ABC has length 8, YZ is not congruent to AB , BC, or AC. Therefore, △ABC is not congruent to △XYZ by the SSS Theorem.

Are △GHI and △WXY congruent?

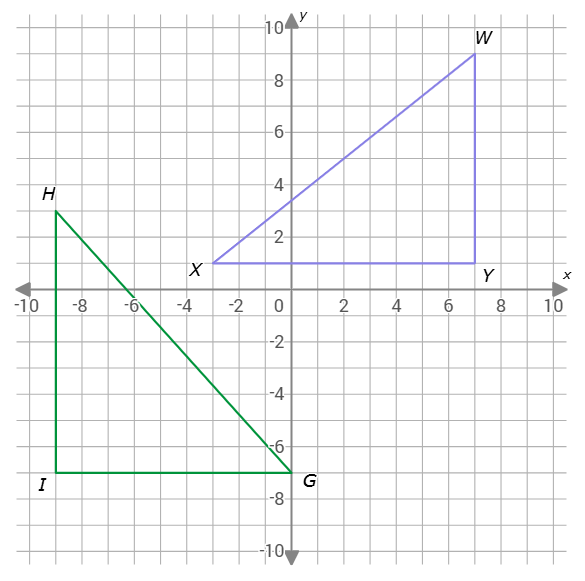
  • yes
  • no

To see that △GHI and △WXY are not congruent, calculate the three side lengths of each triangle.

△GHI has vertices G(0,–7), H(–9,3) and I(–9,–7) and △WXY has vertices W(7,9), X(–3,1) and Y(7,1).

Step 1: Find the side lengths of △GHI.

First, find GI. Since G(0,–7) and I(–9,–7) have the same y-coordinate, GI is the absolute value of the difference in the x-coordinates. So, GI=|–9–0|=9.

Second, find HI. Since H(–9,3) and I(–9,–7) have the same x-coordinate, HI is the absolute value of the difference in the y-coordinates. So, HI=|–7–3|=10.

Third, find GH. Since G(0,–7) and H(–9,3) do not have equal x-coordinates or equal y-coordinates, use the distance formula to calculate GH. Plug in G(0,–7) for (x1,y1) and H(–9,3) for (x2,y2), and simplify.

The three side lengths of △GHI are GI=9, HI=10, and GH=181.

Step 2: Find the side lengths of △WXY.

First, find XY. Since X(–3,1) and Y(7,1) have the same y-coordinate, XY is the absolute value of the difference in the x-coordinates. So, XY=|7– –3|=10.

Second, find WY. Since W(7,9) and Y(7,1) have the same x-coordinate, WY is the absolute value of the difference in the y-coordinates. So, WY=|1–9|=8.

Since no side of △GHI has length 8, WY is not congruent to GI , HI, or GH. Therefore, △GHI is not congruent to △WXY by the SSS Theorem.

Let’s Practice!