SSS, SAS and ASA Theorems
key notes :
🔺 SSS (Side-Side-Side) Congruence Theorem
💡 Statement:
If three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.
📏 Symbolically:
If AB = PQ, BC = QR, and CA = RP 👉 then △ABC ≅ △PQR
🎯 Meaning:
All sides are the same length — so the triangles are exactly the same shape and size!
🧠 Tip:
No need to check angles — sides are enough! ✅
📐 SAS (Side-Angle-Side) Congruence Theorem
💡 Statement:
If two sides and the included angle (the angle between those sides) of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
📏 Symbolically:
If AB = PQ, ∠B = ∠Q, and BC = QR 👉 then △ABC ≅ △PQR
🎯 Meaning:
Two equal sides with the angle between them equal ensure both triangles are identical.
🧠 Remember:
The included angle must be the one between the two sides — not outside them! 🔺
📏 ASA (Angle-Side-Angle) Congruence Theorem
💡 Statement:
If two angles and the included side (the side between the angles) of one triangle are equal to the corresponding parts of another triangle, then the triangles are congruent.
📏 Symbolically:
If ∠A = ∠P, AB = PQ, and ∠B = ∠Q 👉 then △ABC ≅ △PQR
🎯 Meaning:
Two angles and the side between them determine the triangle completely.
🧠 Tip:
Angles + the included side = perfect match! 💯
💫 Why Congruence Matters
✅ Congruent triangles have equal sides and equal angles.
✅ Used to prove geometric results, construct figures, and solve real-world problems.
✅ Congruence helps us understand symmetry and similarity in shapes! 🌍
🌈 Quick Recap Table:
| 🔢 Theorem | 🧩 Given Equal Parts | 🎯 Condition | 🏆 Result |
|---|---|---|---|
| SSS | 3 sides | All sides equal | Triangles congruent |
| SAS | 2 sides + included angle | Angle between sides equal | Triangles congruent |
| ASA | 2 angles + included side | Side between angles equal | Triangles congruent |
🧭 Bonus Tip:
When triangles are congruent (≅), their corresponding parts are equal — this is called CPCTC (Corresponding Parts of Congruent Triangles are Congruent)! 🏅
Learn with an example
Which rule explains why these triangles are congruent?
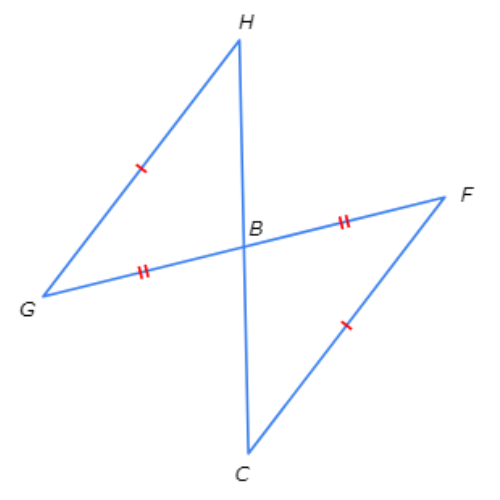
- ASA
- SSS
- SAS
- These triangles cannot be proven congruent.
First, look for congruent sides and angles.
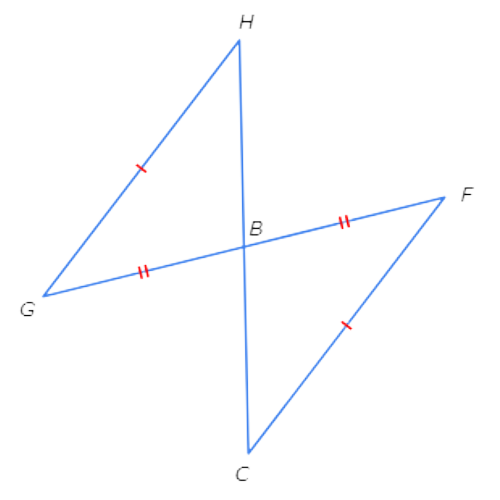
CF ≅ GH and BF ≅ BG .
Next, notice that ∠CBF and ∠GBH are vertical angles. Since vertical angles are congruent, ∠CBF≅∠GBH.
Finally, put the three congruency statements in order. BF is between CF and ∠CBF, and BG is between GH and ∠GBH in the diagram.
CF ≅ GH Side
BF ≅ BG Side
∠CBF ≅ ∠GBH Angle
In order, the congruent sides and angles form SSA. This is not one of the three ways to show that triangles are congruent. There is not enough information to prove that the triangles are congruent.
Which rule explains why these triangles are congruent?
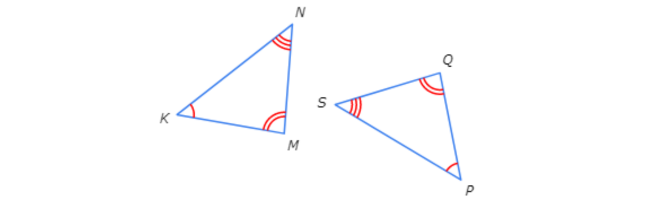
- SSS
- SAS
- ASA
- These triangles cannot be proven congruent.
First, look for congruent sides and angles.
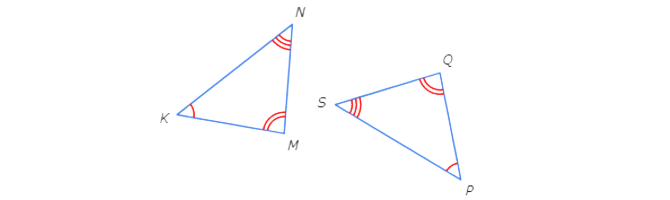
Notice that there are no pairs of congruent sides. Since all of the congruency theorems call for at least one pair of congruent sides, there is not enough information to prove that the triangles are congruent.
Which rule explains why these triangles are congruent?
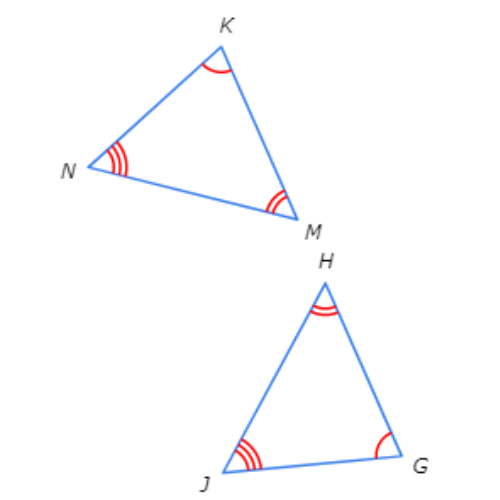
- ASA
- SAS
- SSS
- These triangles cannot be proven congruent.
First, look for congruent sides and angles.
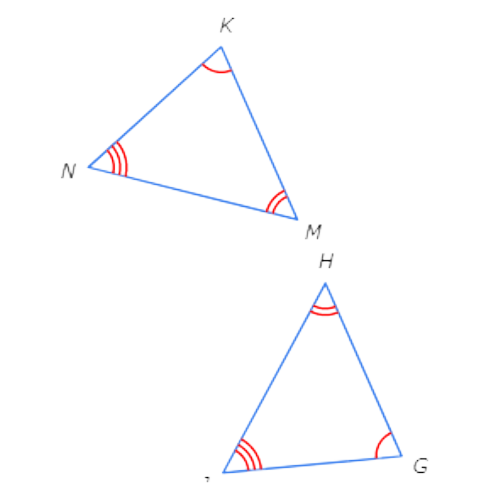
Notice that there are no pairs of congruent sides. Since all of the congruency theorems call for at least one pair of congruent sides, there is not enough information to prove that the triangles are congruent.
Let’s practice!✍️

