Midsegments of triangles

key notes :

Definition of Midsegment

  • A midsegment of a triangle is a segment that connects the midpoints of two sides of the triangle.

Midsegment Theorem

  • The midsegment of a triangle is parallel to the third side.
  • The length of the midsegment is half the length of the third side.

Properties of Midsegments

  • Every triangle has three midsegments, each connecting the midpoints of two sides.
  • The midsegments divide the triangle into four smaller triangles, all of which are similar to the original triangle.
  • The smaller triangles formed have the same angles as the original triangle.

Formula for the Midsegment

  • If the third side of the triangle is AB, and the midsegment is MN, then:

MN = 1/2 AB

Application of Midsegments

  • Used in coordinate geometry to find midpoints and slopes.
  • Helps in proving triangle similarity and parallel lines.
  • Useful in construction and design, such as bridges and support structures.

Example Problem

  • Given a triangle where the third side is 10 cm, the midsegment will be 5 cm long.
  • If a midsegment is 6 cm, the third side is 12 cm.

Learn with an example

SU is a midsegment of △TVW.

If VW=44, what is SU?

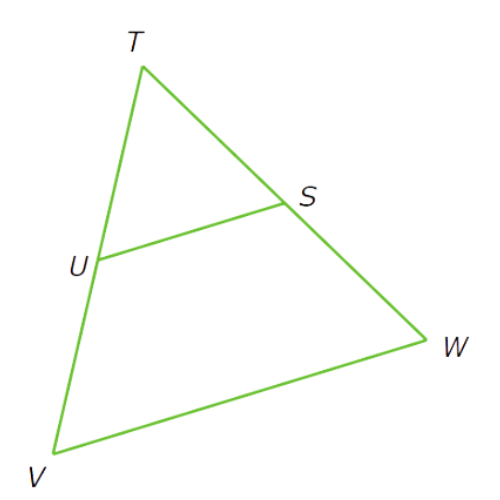
SU =

SU is a midsegment of △TVW.

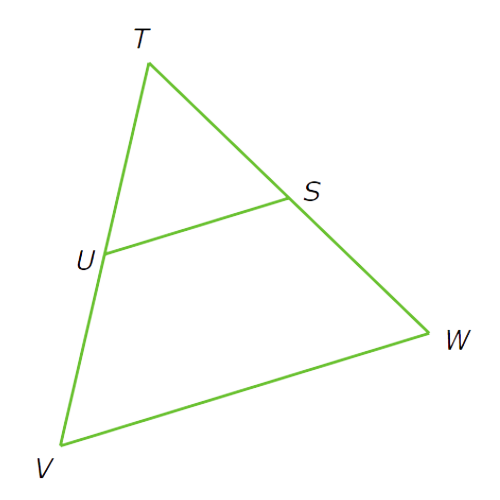
So, SU is half of VW. Set SU equal to half of VW and solve for SU.

SU=VW/2

=44/2 —> Plug in VW=44

=22 —>Divide

So, SU=22.

If PR=20, what is ST?

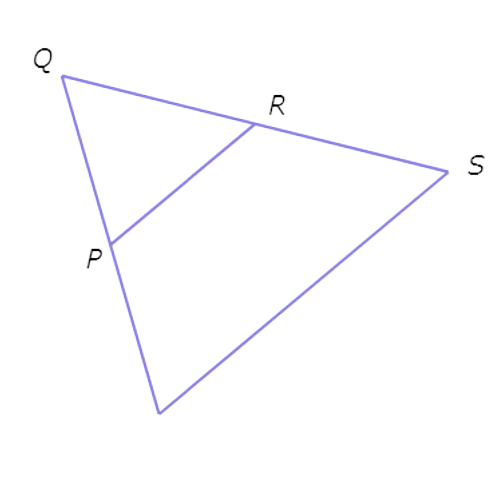
ST= ____

Since P is the midpoint of QT and R is the midpoint of QS . PR is a midsegment of △QST.

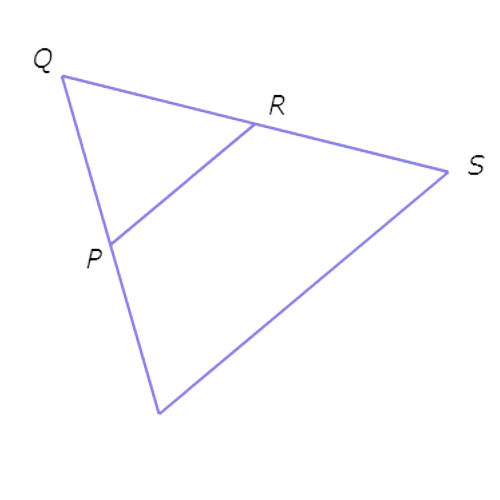
So, PR is half of ST. In other words, ST is twice PR. Set ST equal to twice PR and solve for ST.

ST= 2 . PR

= 2(20) Plug in PR=20

= 40 Multiply

So, ST=40.

If PR=35, what is ST?

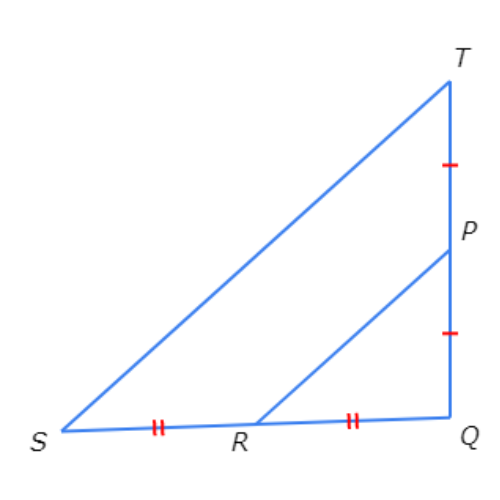
ST=

Since PT ≅ PQ and RS ≅ QR , PR is a midsegment of △QST.

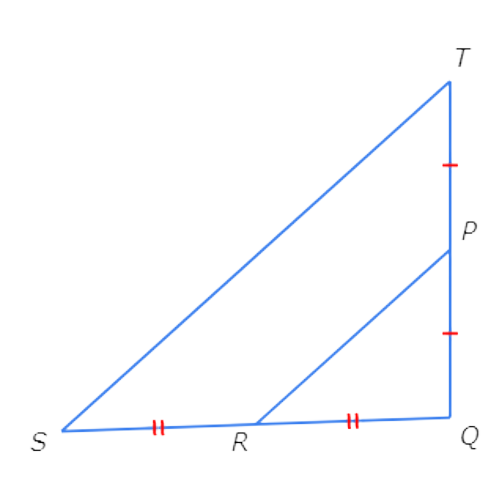
So, PR is half of ST. In other words, ST is twice PR. Set ST equal to twice PR and solve for ST.

ST = 2 . PR

= 2(35) Plug in PR=35

= 70 Multiply

So, ST=70.

Let’s try some problems!✍️