Angle-side relationships in triangles

key notes :

Basic Concept

  • The size of an angle in a triangle is directly related to the length of the opposite side.

Longest Side – Largest Angle Relationship

  • In any triangle, the longest side is opposite the largest angle.
  • The shortest side is opposite the smallest angle.

Triangle Inequality Theorem

  • The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Ordering Sides and Angles

  • If given a triangle with three angles, the side opposite the largest angle is the longest, and the side opposite the smallest angle is the shortest.

Angle-Side Relationships in Special Triangles

  • Right Triangle: The hypotenuse (longest side) is always opposite the 90° angle.
  • Isosceles Triangle: The two equal sides are opposite two equal angles.
  • Equilateral Triangle: All three sides and angles are equal (each angle = 60°).

Converse of the Angle-Side Relationship

  • If a triangle has three unequal sides, then the largest angle will be opposite the longest side, and the smallest angle will be opposite the shortest side.

Application in Problem-Solving

  • Used to compare side lengths and angles in different triangles.
  • Helpful in determining unknown side lengths or angles using given information.

Learn with an example

Find the largest angle of △VWX.

∠ _____

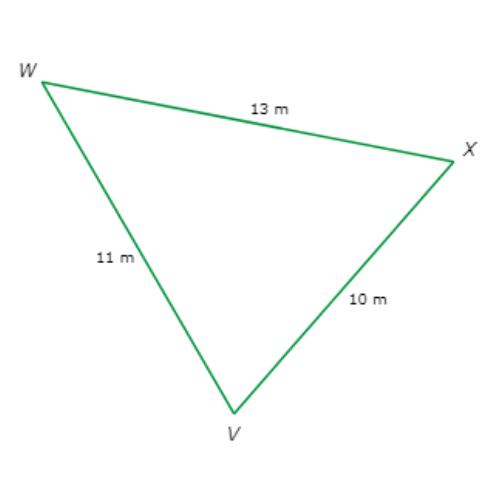
The side lengths are VX=10 metres, VW=11 metres, and WX=13 metres. Since 10 < 11 < 13, VX < VW < WX.

Their opposite angles are in the same order, from smallest to largest:

∠W < ∠X < ∠V

So, the largest angle is ∠V.

Find the largest angle of △GHI.

∠ ______

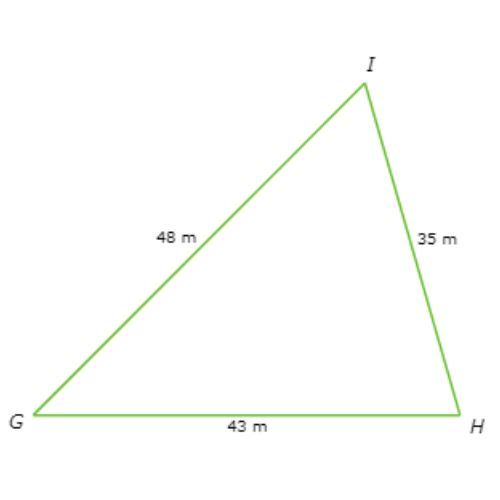
The side lengths are HI=35 metres, GH=43 metres, and GI=48 metres. Since 35 < 43 < 48, HI < GH < GI.

Their opposite angles are in the same order, from smallest to largest:

∠G < ∠I < ∠H

So, the largest angle is ∠H.

Find the largest angle of △UVW.

∠ ___

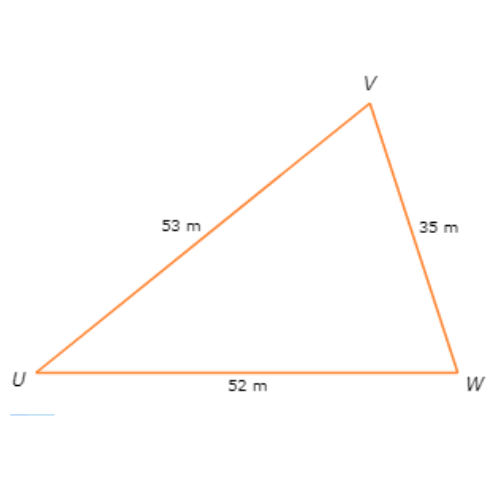
The side lengths are VW=35 metres, UW=52 metres, and UV=53 metres. Since 35 < 52 < 53, VW < UW < UV.

Their opposite angles are in the same order, from smallest to largest:

∠U < ∠V < ∠W

So, the largest angle is ∠W.

Let’s practice!