Hypotenuse-Leg Theorem
key notes :
🔹 What is the Hypotenuse–Leg Theorem?
👉 The HL Theorem applies only to right triangles ⏫.
It states that:
🧠 If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
✳️ In short:
If two right triangles have the same hypotenuse and one leg equal ➡️ they are congruent triangles! 🔺=🔺
🔹 Conditions for HL Theorem 🧩
To use the HL Theorem, make sure these are true:
✅ Both triangles are right triangles
✅ The hypotenuse of one is congruent to the hypotenuse of the other
✅ One leg of one triangle is congruent to one leg of the other
🔹 Why It Works 🧠
The HL Theorem is actually a special case of the SSS (Side-Side-Side) or SAS (Side-Angle-Side) postulates because the right angle is already known (90°). ⦜
🟩 The right angle acts as the included angle! 🎯
🔹 Formula Reminder 💡
There’s no direct formula, but remember:
HL ≈ “Right triangle + Hypotenuse + Leg = Congruent Triangles”
Example:
If in △ABC and △DEF,
- ∠C and ∠F are right angles
- AB ≅ DE (hypotenuse)
- BC ≅ EF (leg)
✅ Then, △ABC ≅ △DEF by HL Theorem 🎉
🔹 Diagram Tip 🖊️
Draw two right triangles side by side:
- Mark one side as the leg 🦵
- Mark the longest side as the hypotenuse 🔺
- Show congruency with “≅” marks to visualize the theorem! 👀
🔹 Real-Life Connection 🌍
The HL Theorem helps in:
🏗️ Designing ramps or right-angled supports
📐 Verifying structures like ladders leaning against walls
🎯 Engineering and architecture designs that involve right triangles
🔹 Fun Memory Trick! 🎲
💬 “HL = Hypotenuse + Leg = Right Triangles Match!”
🧡 HL → “Helpful in Right triangles” 😄
📘 Summary:
| 🔹Condition | 🔹Meaning |
|---|---|
| Both are right triangles ⦜ | Each has a 90° angle |
| Hypotenuse congruent | Longest sides equal |
| One leg congruent | One shorter side equal |
| 🟰 | Triangles are congruent (HL) |
✨ Example Question:
If △ABC and △DEF are right triangles with
- Hypotenuse AB = DE
- Leg BC = EF
➡️ Then, △ABC ≅ △DEF by HL Theorem ✅
Learn with an example
What values of v and w make △FGH ≅ △DCE?
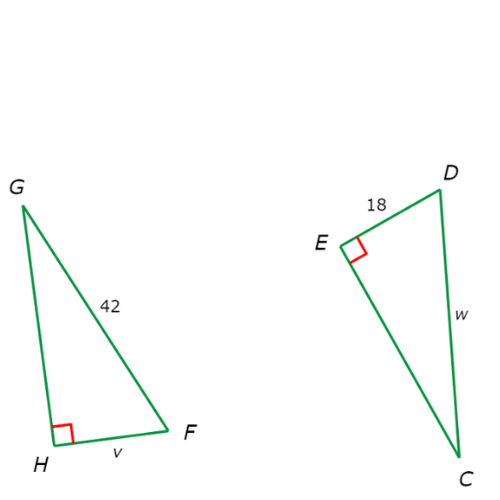
v = _____
w = _____
Use the Hypotenuse-Leg Theorem to solve for the values of v and w that make the triangles congruent.
First, look at the labelled pair of corresponding legs. The first leg FH has a length of v and the second leg DE has a length of 18. For the triangles to be congruent, the leg lengths must be equal. So, v must equal 18.
Now, look at the hypotenuses. The first hypotenuse FG has a length of 42 and the second hypotenuse DC has a length of w. For the triangles to be congruent, the hypotenuse lengths must be equal. So, w must equal 42.
The values of v and w that make △FGH ≅ △DCE are v=18 and w=42.
What values of x and y make △GHI ≅ △EDF?
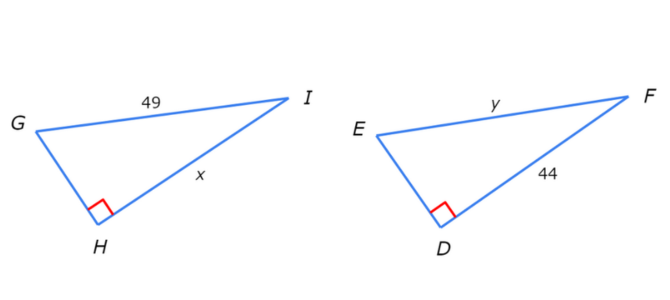
X =
Y =
Use the Hypotenuse-Leg Theorem to solve for the values of x and y that make the triangles congruent.
First, look at the labelled pair of corresponding legs. The first leg HI has a length of x and the second leg DF has a length of 44. For the triangles to be congruent, the leg lengths must be equal. So, x must equal 44.
Now, look at the hypotenuses. The first hypotenuse GI has a length of 49 and the second hypotenuse EF has a length of y. For the triangles to be congruent, the hypotenuse lengths must be equal. So, y must equal 49.
The values of x and y that make △GHI≅△EDF are x=44 and y=49.
Let’s try some problems!✍️

