Identify complementary, supplementary, vertical, adjacent and congruent angles
Key Notes:
| Introduction to Angles |
An angle is formed when two rays share a common endpoint. The rays are called sides of the angle, and the common endpoint is called the vertex. Angles are measured in degrees (°).
| Types of Angle Relationships |
Complementary Angles
Definition: Two angles are complementary if the sum of their measures is 90°.
- Formula:
- Angle A+Angle B=90∘
- Example:
- ∠P = 30°, ∠Q = 60° → ∠P + ∠Q = 90° → Complementary
Key Tip: Each angle is called the complement of the other.
Supplementary Angles
- Definition: Two angles are supplementary if the sum of their measures is 180°.
- Formula:
- Angle A+Angle B=180∘
- Example:
∠X = 110°, ∠Y = 70° → ∠X + ∠Y = 180° → Supplementary - Key Tip: Often seen in a straight line.
Vertical Angles (Opposite Angles)
- Definition: Vertical angles are formed when two lines intersect, creating two pairs of opposite angles.
- Property: Vertical angles are always equal.
- Example:
If ∠1 = 50°, then the angle opposite to it ∠2 = 50° - Key Tip: Also called opposite angles.
Adjacent Angles
- Definition: Adjacent angles share a common vertex and a common side, but do not overlap.
- Property: The sum of adjacent angles may or may not be 90° or 180° (depends on the situation).
- Example:
∠A and ∠B share a vertex O and a common side → Adjacent
Congruent Angles
- Definition: Congruent angles have the same measure.
- Symbol: ∠A ≅ ∠B
- Example:
∠P = 40°, ∠Q = 40° → ∠P ≅ ∠Q - Key Tip: Congruent angles can be anywhere, not necessarily adjacent.
| Quick Reference Table |
| Angle Type | Definition | Formula / Property | Example |
|---|---|---|---|
| Complementary | Sum = 90° | A + B = 90° | 30° + 60° |
| Supplementary | Sum = 180° | A + B = 180° | 110° + 70° |
| Vertical | Opposite angles when lines intersect | ∠1 = ∠2 | 50° and opposite 50° |
| Adjacent | Share a vertex and a side | May vary | ∠A and ∠B share vertex O |
| Congruent | Same measure | ∠A ≅ ∠B | 40° ≅ 40° |
| Tips to Identify |
- Look at the sum → 90° (complementary), 180° (supplementary).
- Look at the position → Opposite angles (vertical), side by side (adjacent).
- Compare measures → Same measure → Congruent.
| Practice Questions |
- Find the complement of 35°.
- Two angles are supplementary. If one angle is 120°, find the other.
- Identify the vertical angles in an intersecting lines diagram.
- Find which angles are adjacent in the given figure.
- Check if two angles measuring 55° and 55° are congruent.
Adjacent angles share a vertex and a side, but no interior points.

Congruent angles have the same measure.
Vertical angles are angles formed opposite each other when two lines intersect. Vertical angles are congruent.
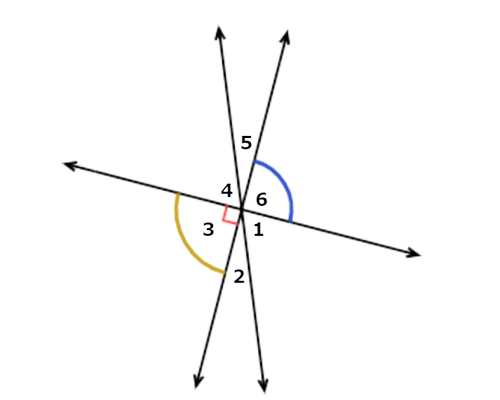
∠6 and ∠3 are congruent. They are vertical angles, which have the same measure.
Complementary angles have measures that add to 90°.
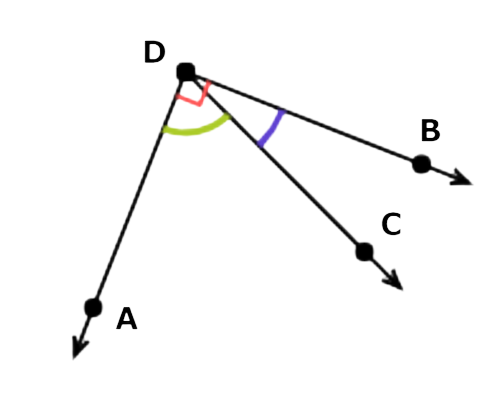
The angle that is complementary to ∠CDA is ∠BDC. Together they form a right angle, so their angles add up to 90°.
Angles complementary to ∠CDA include ∠BDC.
Supplementary angles have measures that add to 180°.
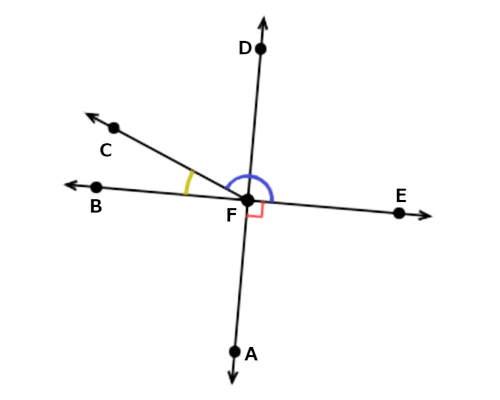
∠BFC is supplementary to ∠CFE. Together they form a straight line, which has a measure of 180°. So, their angles add up to 180°.
Learn with an example
Which angles are congruent to ∠EFA? Select all that apply.
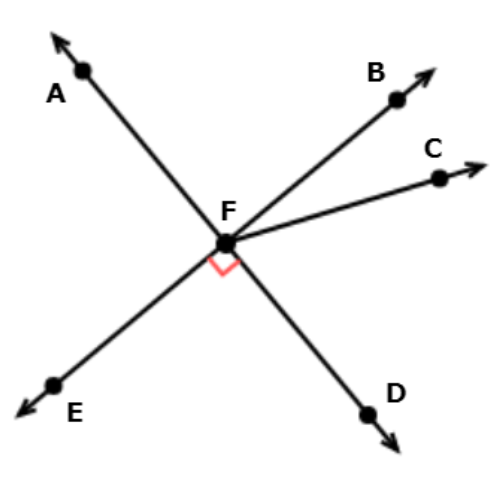
- ∠CFD
- ∠CFE
- ∠AFC
- ∠AFB
Look at ∠EFA and ∠
∠AFB and ∠EFA are congruent. They both measure 90°.
What is an angle that is adjacent to ∠1?
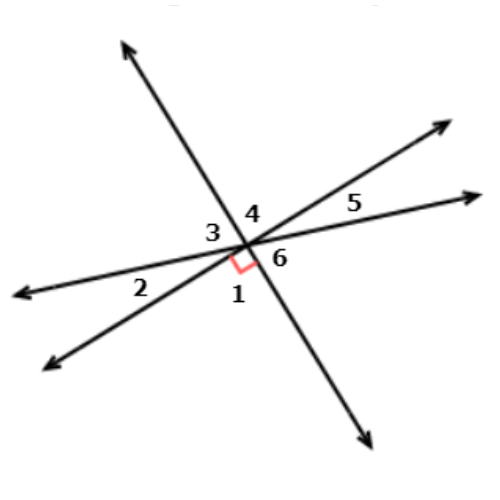
∠ ___
Look at ∠1:
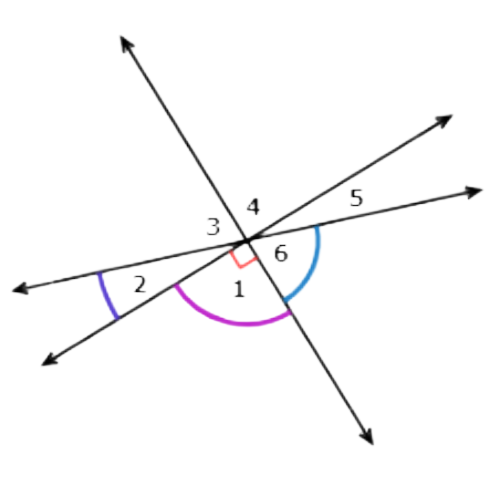
One angle that is adjacent to ∠1 is ∠2.
The other angle that is adjacent to ∠1 is ∠6.
Angles adjacent to ∠1 include ∠2 and ∠6.
Which angle is congruent to ∠2 ?
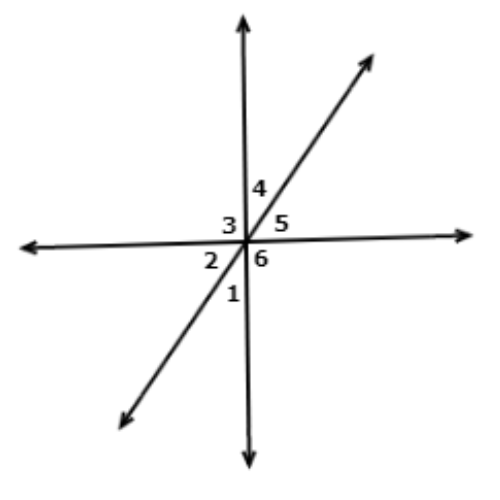
- ∠4
- ∠6
- ∠5
- ∠3
Look at ∠2 and ∠5:
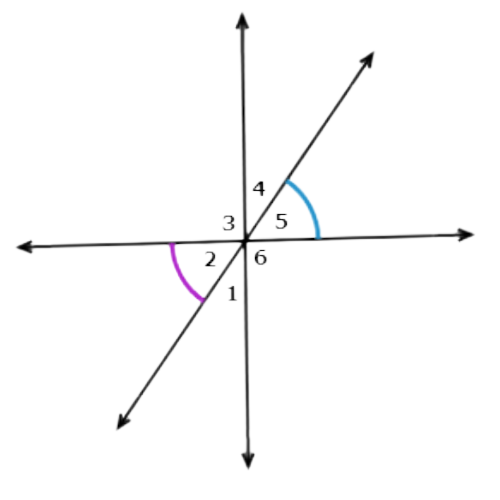
∠5 and ∠2 are congruent. They are vertical angles, which have the same measure.
Let’s Practice!

